这里是一些轨道动力学中常见物理量的计算机算法的总结。
本文公式较多,在浏览器中将会花较长时间用于渲染公式。
最近专业课又是轨道动力学又是姿态动力学什么的,非常有意思。在航天器动力学里面有太多的算法可以讲,从时间转换、坐标系的转换到轨道外推这些,刚体动力学其实还可以借鉴游戏引擎的一些思路。自己最近借学习这些课程的机会,自己实现了3维向量、3阶方阵、四元数的轮子。关于刚体动力学,在航天中也就是姿态动力学的探讨不在本文。这篇文章总结一些轨道动力学常见物理量的算法。
笛卡尔坐标系转换到轨道六根数
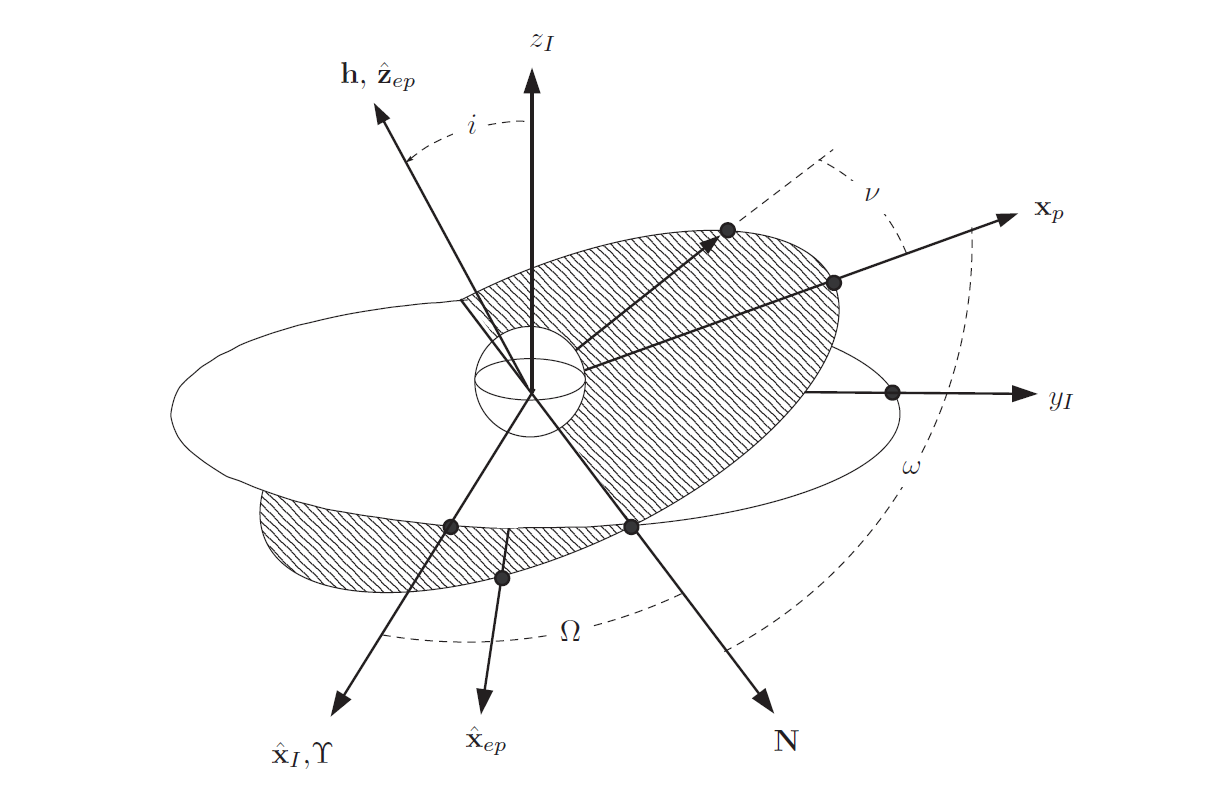
- 已知:$\mathbf{r},\mathbf{v}$和引力常数$\mu$
- 求:$a,e,i,\omega,\Omega,\nu$
\begin{equation} \mathbf{h} = \mathbf{r}\times\mathbf{v}\end{equation}
\begin{equation} h = ||\mathbf{h}||\end{equation}
升交线方向的矢量是
\begin{equation} \mathbf{n}=[0,0,1]^T\times\mathbf{h}\end{equation}
\begin{equation} n = ||\mathbf{n}||\end{equation}
轨道的离心率和能量通过以下式子计算
\begin{equation} \mathbf{e} = \frac{(v^2-\frac{\mu}{r})\mathbf{r}-(\mathbf{r}\cdot\mathbf{v})\mathbf{v}}{\mu}\end{equation}
\begin{equation}e=||\mathbf{e}||\end{equation}
\begin{equation}\xi = \frac{v^2}{2}-\frac{\mu}{r}\end{equation}
对于抛物线轨道,半长轴是正无穷而能量是0.这里要做的工作是检查轨道是否是近抛物线轨道。如果$|1-e|<10^{-7}$,就要另外讨论了。
半长轴的计算公式为
\begin{equation}a=-\frac{\mu}{2\xi}\end{equation}
轨道倾角:
\begin{equation}i=\arccos(\frac{h_z}{h})\end{equation}
计算升交点赤经,近地点角距,真近点角需要分四种情况处理
情况1:对于非圆,非赤道平面的轨道
如果$(e \geq 10^{−11}),(10^{−11} \leq i \leq \pi − 10^{−11})$,升交点赤经
\begin{equation}\Omega=\arccos(\frac{n_x}{n})\end{equation}
但是如果$n_y<0$,那么$\Omega = 2\pi-\Omega$
近地点角距
\begin{equation}\omega=\arccos(\frac{\mathbf{n}\cdot\mathbf{e}}{ne})\end{equation}
如果$e_z<0$,那么$\omega = 2\pi-\omega$
真近点角
\begin{equation}\nu=\arccos(\frac{\mathbf{e}\cdot\mathbf{r}}{er})\end{equation}
如果$\mathbf{r}\cdot\mathbf{v}<0$,那么$\nu=2\pi-\nu$
情况2:对于非圆,在赤道平面的轨道
如果$(e \geq 10^{−11}),(10^{−11} \geq i)|(i \geq \pi − 10^{−11})$,那么
\begin{equation}\Omega=0\end{equation}
\begin{equation}\omega=\arccos(\frac{\mathbf{n}\cdot\mathbf{e}}{ne})\end{equation}
但是如果$e_y<0$,那么$\omega = 2\pi-\omega$
\begin{equation}\nu=\arccos(\frac{\mathbf{e}\cdot\mathbf{r}}{er})\end{equation}
如果$\mathbf{r}\cdot\mathbf{v}<0$,那么$\nu=2\pi-\nu$
情况3:对于圆,非赤道平面的轨道
如果$(e \leq 10^{−11}),(10^{−11} \leq i \leq \pi − 10^{−11})$,那么
\begin{equation}\Omega=\arccos(\frac{n_x}{n})\end{equation}
但是如果$n_y<0$,那么$\Omega = 2\pi-\Omega$
\begin{equation}\omega=0\end{equation}
\begin{equation}\nu=\arccos(\frac{\mathbf{e}\cdot\mathbf{r}}{er})\end{equation}
如果$r_z<0$,那么$\nu=2\pi-\nu$
情况4:对于圆,在赤道平面的轨道
如果$(e \leq 10^{−11}),(10^{−11} \geq i)|(i \geq \pi − 10^{−11})$,那么
\begin{equation}\Omega=0\end{equation}
\begin{equation}\omega=0\end{equation}
\begin{equation}\nu=\arccos(\frac{r_x}{r})\end{equation}
如果$r_y<0$,那么$\nu=2\pi-\nu$
轨道六根数转换到笛卡尔坐标系
- 已知:$a,e,i,\omega,\Omega,\nu$ 和引力常数$\mu$
- 求: $\mathbf{r},\mathbf{v}$
首先是焦准距 \begin{equation}p=a(1-e^2)\end{equation} \begin{equation}r=\frac{p}{1+e\cos\nu}\end{equation} \begin{equation}x=r(\cos(\omega+\nu)\cos\Omega-\cos i\sin(\omega+\nu)\sin\Omega)\end{equation} \begin{equation}y=r(\cos(\omega+\nu)\sin\Omega+\cos i\sin(\omega+\nu)\cos\Omega)\end{equation} \begin{equation}z=r[\sin(\omega+\nu)\sin i]\end{equation} 这个算法计算计算速度向量的前提是非抛物线轨道,也就是当($||\mathbf{p}||\geq1e-30$),有 \begin{equation}\dot x=\sqrt\frac{\mu}{p}(\cos\nu+e)(-\sin\omega\cos\Omega-\cos i\sin\Omega\cos\omega)-\sqrt\frac{\mu}{p}\sin{\nu}(\cos\omega\cos\Omega-\cos i\sin\Omega\sin\omega)\end{equation} \begin{equation}\dot y=\sqrt\frac{\mu}{p}(\cos\nu+e)(-\sin\omega\sin\Omega+\cos i\cos\Omega\cos\omega)-\sqrt\frac{\mu}{p}\sin{\nu}(\cos\omega\sin\Omega+\cos i \cos\Omega\sin\omega)\end{equation} \begin{equation}\dot z=\sqrt\frac{\mu}{p}[(\cos\nu+e)\sin i\cos\omega-\sin\nu\sin i\sin\omega]\end{equation}
注意这些公式带入运算时都是要化成弧度的!!!