姿态动力学仿真系统

发表于 | 分类于

实现了一个卫星姿态动力学的仿真程序，包括动力学的仿真以及3维显示。

本文公式较多，在浏览器中将会花较长时间用于渲染公式。

这篇文章参考了不少叶劲峰（Milo Yip）大神翻译的经典著作《游戏引擎架构》，以及SimTK引擎的文档。

常见算法

刚体动力学问题里面最容易遇到的就是微分方程，数值求解微分方程最经典的方法莫过于欧拉法和RK4方法，这里就不多说了。不过，游戏引擎里还经常有一种算法：韦尔莱积分（Verlet intergration）。

韦尔莱积分

推导如下：




这里速度就被消去了。

还有一种速度韦尔莱：

  1. $r(t_1+\Delta t)=r(t_1)+v(t_1)\Delta t+\frac{1}{2}a(t_1)\Delta t^2$
  2. $v(t_1+\frac{1}{2}\Delta t)=v(t_1) + \frac{1}{2}a(t_1)\Delta t$
  3. $a(t_1+\Delta t) = m^{-1}F(t_2,r(t_2),v(t_2))$
  4. $v(t_1+\Delta t) = r(t_1+\frac{1}{2}\Delta t) + \frac{1}{2}a(t_1+\Delta t)\Delta t$

这个第三步实际上也用的是近似值，我感觉和CFD中的麦考马克法有些类似。虽然这里是速度，位移，但是同样适用于角度，角速度的情况。

龙格库塔算法

韦尔莱积分具有兼顾速度和精度的特点，因此在游戏引擎中得到了大量运用。但是如果对于需要精确预测的问题，或许还是需要龙格库塔算法。经典龙格库塔法我就不写了，这里写一下更一般的龙格库塔方法。

令初值问题表述如下。

那么 其中





要给定一个特定的方法，必须提供整数$s$（级数），以及系数 $a_{ij}$（对于1 ≤ $j < i$ ≤ s）,$b_i$（对于$i = 1, 2, …, s$）和$c_i$（对于$i = 2, 3, …, s$）。这些数据通常排列在一个助记工具中，称为Butcher tableau（得名自John C. Butcher）：
例如，RK4法可以表示为
欧拉法可以表示为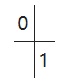： 而下面给出的是Prince-Dormand 45系数： Runge-Kutta-Fehlberg 56系数：

四元数

\begin{equation} q = [\mathbf{q}_v\quad q_s]=[\mathbf{a}\sin\frac{\theta}{2}\quad\cos\frac{\theta}{2}] \end{equation} 其中：

  • $\mathbf{a}$是旋转轴，模长单位化
  • $\frac{\theta}{2}$是旋转半角

四元数的共轭四元数是 \begin{equation} q^{*}=[-\mathbf{q}_v\quad q_s] \end{equation} 容易证明，当$|q|=1$时，$q^{-1}=q^{*}$

四元数表示向量的旋转：例如将向量$\mathbf{v}$写成四元数$v=[\mathbf{v}\quad 0]=[v_x\quad v_y\quad v_z 0]$，则有 \begin{equation} v^{\prime}=rotate(q,\mathbf{v}) = qvq^{-1} \end{equation} 对于刚体，在刚体坐标系下取例如$\mathbf{F_M}=[0\quad 0\quad 1]$，则在惯性系中，

刚体的姿态动力学方程及求解算法

就算一个刚体在没有外力的情况下旋转，在三维旋转动力学中，其角速度矢量$\mathbf{\omega}$可能并不是常亮，转轴会不停地改变方向。以长方体为例，其绕最短或最长轴旋转时，能产生均角速度矢量，而以中间长度的轴旋转，$\mathbf{\omega}$的方向就会改变。
刚体的角动量守恒 \begin{equation} \mathbf{L}=\mathbf{I\omega(t)} \end{equation} 而$\mathbf{\omega}$不守恒。
三维旋转不能直接求解$\mathbf{\omega}$，而应该按照如下方式求解： \begin{equation} \mathbf{\dot L}(t)=\mathbf{N}(t) \end{equation} \begin{equation} \mathbf{\omega}(t)=\mathbf{I^{-1}L}(t) \end{equation} 下面两个方程是四元数的方程： \begin{equation} \omega(t)=[\omega_x\quad \omega_y\quad \omega_z\quad 0] \end{equation} \begin{equation} \frac{1}{2}\omega(t)q(t)=\dot q(t) \end{equation} $q$是定向四元数，表示刚体的定向，$\omega$是角速度四元数。

而惯性张量的坐标变换则是 \begin{equation} \mathbf{I^{\prime}=AIA^T} \end{equation}

齐次坐标

如果定义齐次坐标，则平移运算也可以转化为旋转运算：$\mathbf{r}=[r_x\quad r_y\quad r_z\quad 1]$，若在$\mathbf{r}$向量上平移$\mathbf{s}$，则可以表示为

别的观点

一个刚体的质量特性包括刚体的质量$m$，质心的位置向量$\mathbf{p}$，以及惯性张量$\mathbf{I}$或者$\mathbf{J}$.如果定义回转张量$\mathbf{G}$满足$\mathbf{J}=m\mathbf{G}$，那么一个刚体的特性可以被如下的$6\times6$矩阵描述： 类似的，定义关于质心的空间速度矢量$V^C=\begin{bmatrix}\mathbf{\omega}\ \mathbf{V_C}\end{bmatrix}$，就可以类似的定义动量$P^C=M^CV^C$和动能$KE=\frac{1}{2}V^TMV$ 这样定义以后，关于空间坐标转换有一些好的性质，不过这些公式较为复杂，MathJax的渲染能力有限，我就不写在这里了。具体可以参见SimTK的文档。

编写程序

对于姿态动力学问题，还是需要求解微分方程，需要用到龙格库塔算法。
定义一个简单的，但以后还可以扩展的刚体类

class rigidBody {
public:
    rigidBody();
    rigidBody(double Ix, double Iy, double Iz, mat33 &cosineMat, vec3 &omega,
              std::function<vec3(vec3 &, mat33 &, double)> mome)
        : m_Ix(Ix), m_Iy(Iy), m_Iz(Iz), m_inertia(mat33::fromDiag(Ix, Iy, Iz)),
          m_cosMat(cosineMat), m_omega(omega), m_time(.0), moment(mome) {}
    ~rigidBody() {}

    void do_step(double dt); // calculate the state after time dt

    double getRotKineticEnergy();
    vec3 getAngularMomentum(); // expressed in the inertial frame
    vec3 getOmega();           // expressed in the inertial frame
    mat33 getInertiaTensor();  // expressed in the inertial frame
    mat33 getCosineMat();

private:
    // double m_mass;
    double m_Ix, m_Iy, m_Iz;
    mat33 m_inertia; // expressed in the body frame
    mat33 m_cosMat;
    // vec3 m_pos;
    vec3 m_omega; // expressed in the body frame
    // vec3 m_speed;
    double m_time;
    std::function<vec3(vec3 &, mat33 &, double)> moment;
    // suppose M=M(omega,cosineMatrix,t), expressed in the body frame
    // vec3 force(parameters);

    void func(double t, vec3 &omega, mat33 &cosMat, vec3 &resVec,
              mat33 &resMat);
    // get the diff format of the moment dynamics
};

代码中都有具体的注释解释。我实现的动力学的时间步进代码如下：

void rigidBody::func(double t, vec3 &vec, mat33 &cosMat, vec3 &resVec,
                     mat33 &resMat) {
    vec3 M = moment(vec, cosMat, t);
    double dwx =
        M.getX() / m_Ix + vec.getY() * vec.getZ() / m_Ix * (m_Iz - m_Iy);
    double dwy =
        M.getY() / m_Iy + vec.getX() * vec.getZ() / m_Iy * (m_Ix - m_Iz);
    double dwz =
        M.getZ() / m_Iz + vec.getX() * vec.getY() / m_Iz * (m_Iy - m_Ix);
    resVec = vec3(dwx, dwy, dwz);

    resMat = crossProductMat3(vec) * cosMat;
}

void rigidBody::do_step(double dt) {
    // using RK4 algorithm

    static vec3 vk1, vk2, vk3, vk4;
    static mat33 mk1, mk2, mk3, mk4;
    static vec3 resV;
    static mat33 resM;

    double t = m_time;

    func(t, m_omega, m_cosMat, vk1, mk1);
    mk1 *= dt;
    vk1 *= dt;
    resV = m_omega + .5 * vk1;
    resM = m_cosMat + .5 * mk1;

    func(t + .5 * dt, resV, resM, vk2, mk2);
    mk2 *= dt;
    vk2 *= dt;
    resV = m_omega + .5 * vk2;
    resM = m_cosMat + .5 * mk2;

    func(t + .5 * dt, resV, resM, vk3, mk3);
    mk3 *= dt;
    vk3 *= dt;
    resV = m_omega + vk3;
    resM = m_cosMat + mk3;

    func(t + dt, resV, resM, vk4, mk4);
    mk4 *= dt;
    vk4 *= dt;

    m_time += dt;
    m_omega += (.16666666666666666666666666666666666666666666666666666666666 *
                (vk1 + 2.0 * vk2 + 2.0 * vk3 + vk4));
    m_cosMat += (.16666666666666666666666666666666666666666666666666666666666 *
                 (mk1 + 2.0 * mk2 + 2.0 * mk3 + mk4));
}

然后需要绘制3维的动画，这一点也很麻烦。首先需要写一个sceneModifier来显示三维模型：

SceneModifier::SceneModifier(Qt3DCore::QEntity *rootEntity)
    : m_rootEntity(rootEntity) {
    // Cylinder shape data
    Qt3DExtras::QCylinderMesh *cylinder = new Qt3DExtras::QCylinderMesh();
    cylinder->setRadius(1);
    cylinder->setLength(3);
    cylinder->setRings(100);
    cylinder->setSlices(20);

    // CylinderMesh Transform
    Qt3DCore::QTransform *cylinderTransform = new Qt3DCore::QTransform();
    cylinderTransform->setScale(1.5f);
    cylinderTransform->setRotation(
        QQuaternion::fromAxisAndAngle(QVector3D(1.0f, 0.0f, 0.0f), 20.0f));
    cylinderTransform->setTranslation(QVector3D(-5.0f, 4.0f, -1.5));

    Qt3DExtras::QPhongMaterial *cylinderMaterial =
        new Qt3DExtras::QPhongMaterial();
    cylinderMaterial->setDiffuse(QColor(QRgb(0x928327)));

    // Cylinder
    m_satEntity = new Qt3DCore::QEntity(m_rootEntity);
    m_satEntity->addComponent(cylinder);
    m_satEntity->addComponent(cylinderMaterial);
    m_satEntity->addComponent(cylinderTransform);
}

这个例子是从Qt3D的一个example改过来的，Qt3D可以让我们更加方便地绘制3D模型。具体的调用方法很简单，其中光线、材质渲染与这里讨论的主题关系不大，可以不用管。主要是需要对动画涉及的刚体的transform需要制作动画。

void SceneModifier::setSome(int type) {
    delete m_satEntity;
    m_satEntity = new Qt3DCore::QEntity(m_rootEntity);

    Qt3DExtras::QPhongMaterial *satMaterial = new Qt3DExtras::QPhongMaterial();
    satMaterial->setDiffuse(QColor(QRgb(0x928327)));

    // satMesh Transform
    Qt3DCore::QTransform *satTransform = new Qt3DCore::QTransform();
    satTransform->setScale(1.5f);

    satTransform->setTranslation(QVector3D(-5.0f, 4.0f, -1.5));
    TransformController *ctrl = new TransformController(satTransform);
    ctrl->setType(type);
    ctrl->setTarget(satTransform);
    ctrl->setTime(.0f);

    QPropertyAnimation *animation = new QPropertyAnimation(satTransform);
    animation->setTargetObject(ctrl);
    animation->setPropertyName("time");
    animation->setDuration(100000);
    animation->setStartValue(QVariant::fromValue(.0));
    animation->setEndValue(QVariant::fromValue(800000000));
    animation->setLoopCount(1);
    animation->start();

    // sat
    m_satEntity->addComponent(satTransform);
    m_satEntity->addComponent(satMaterial);
}

因此我们需要定义一个TransformController的类：

class TransformController : public QObject {
    Q_OBJECT
    Q_PROPERTY(Qt3DCore::QTransform *target READ target WRITE setTarget NOTIFY
                   targetChanged)
    Q_PROPERTY(float time READ time WRITE setTime NOTIFY timeChanged)

public:
    TransformController(QObject *parent = 0);

    void setTarget(Qt3DCore::QTransform *target);
    Qt3DCore::QTransform *target() const;

    void setTime(float time);
    float time() const;

signals:
    void targetChanged();
    void timeChanged();

protected:
    void updateQuat();

private:
    Qt3DCore::QTransform *m_target;
    QQuaternion m_quat;
    float m_time;
    float dt;

    rigidBody m_body;

    /*mat33 tensor;
    vec3 omega;
    vec3 angularM;
    mat33 cosineMat;*/
};

TransformController中比较关键的几个代码如下：

void TransformController::setTarget(Qt3DCore::QTransform *target) {
    if (m_target != target) {
        m_target = target;
        emit targetChanged();
    }
}

Qt3DCore::QTransform *TransformController::target() const { return m_target; }

void TransformController::setTime(float time) {
    if (!qFuzzyCompare(time, m_time)) {
        dt = (time - m_time) / 12000000.0; // 1000.0;
        // dt=.01;
        m_time = time;
        updateQuat();
        emit timeChanged();
    }
}

float TransformController::time() const { return m_time; }

void TransformController::updateQuat() {
    m_body.do_step(dt);
    m_quat = fromMat33(m_body.getCosineMat());
    m_target->setRotation(m_quat);

    static vec3 am, omega, z_;
    static vec3 z(.0, 1.0, .0);
    z_ = m_body.getCosineMat().transpose() * z;
    // express the vector in the inertial frame
    am = m_body.getAngularMomentum();

    // omega=m_body.getOmega();
    omega = m_body.m_omega;
    double T = m_body.getRotKineticEnergy(), theta = angle(z, z_) * degPerRad;
    // theta is called the nutation angle
}

由于TransformController的类定义有这样一条语句：Q_PROPERTY(float time READ time WRITE setTime NOTIFY timeChanged),因此如果时间变化，就会调用setTime函数，setTime函数会调用updateQuat函数，在updateQuat函数中进行动力学的时间步进求解，而m_target就保存的是刚体的旋转四元数信息，更新之后就会用新的旋转四元数渲染三维模型。