本文对一道悬臂梁的动力学响应问题进行了研究,分别实现了时域方法、时域和频域结合的方法、纯频域方法等多种数值方法,并对不同方法进行了比较。
题目描述
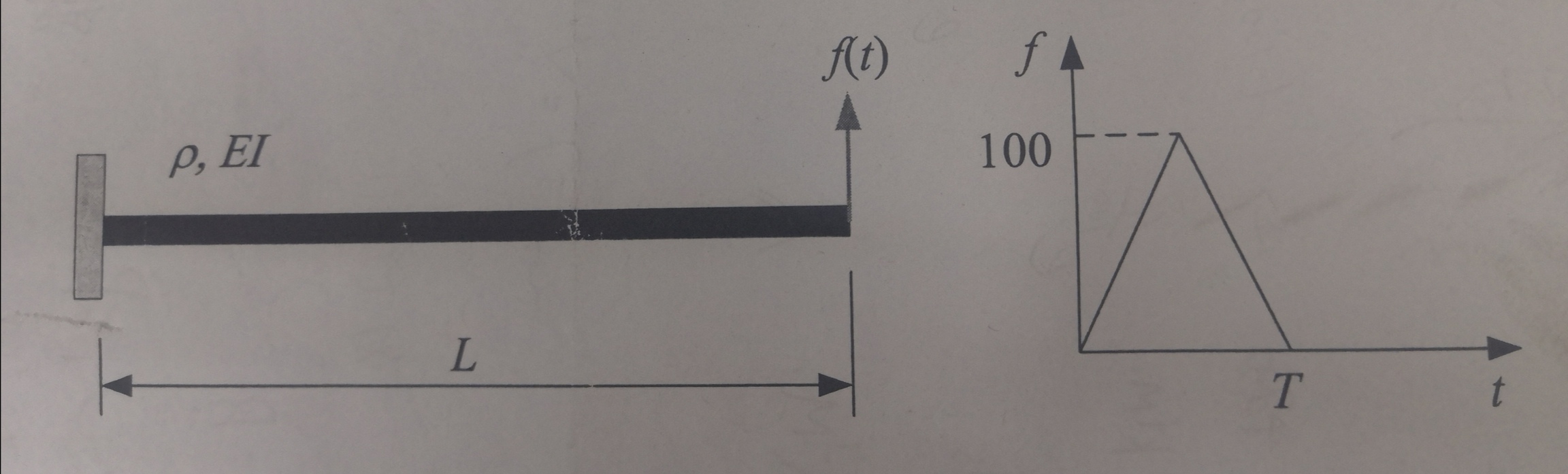 如图所示悬臂梁,长度L=1m,弯曲刚度$EI=10\text{Nm}^2$,线密度$\rho=0.3\text{kg/m}^3$,计算当$T=0.1,0.5,1.0s$时梁在$f(t)$作用下的根部弯矩的时间响应。
如图所示悬臂梁,长度L=1m,弯曲刚度$EI=10\text{Nm}^2$,线密度$\rho=0.3\text{kg/m}^3$,计算当$T=0.1,0.5,1.0s$时梁在$f(t)$作用下的根部弯矩的时间响应。
时域方法
有限元方法
建立梁单元的刚度矩阵为
单元质量矩阵为
将梁分为数个梁单元,边界条件为一端固支。组装有限元方程后,可以通过求$\lambda{\bm{M}^{-1}\bm{K}}$与梁的解析解的固有角频率的平方比较,当划分的网格增大时,特征值趋于梁的解析解的固有角频率的平方,验证有限元模型的正确性。因此写出有限元的动力学方程: \begin{equation} \bm{M}\bm{\ddot x}+\bm{Kx}=\bm{f} \end{equation}
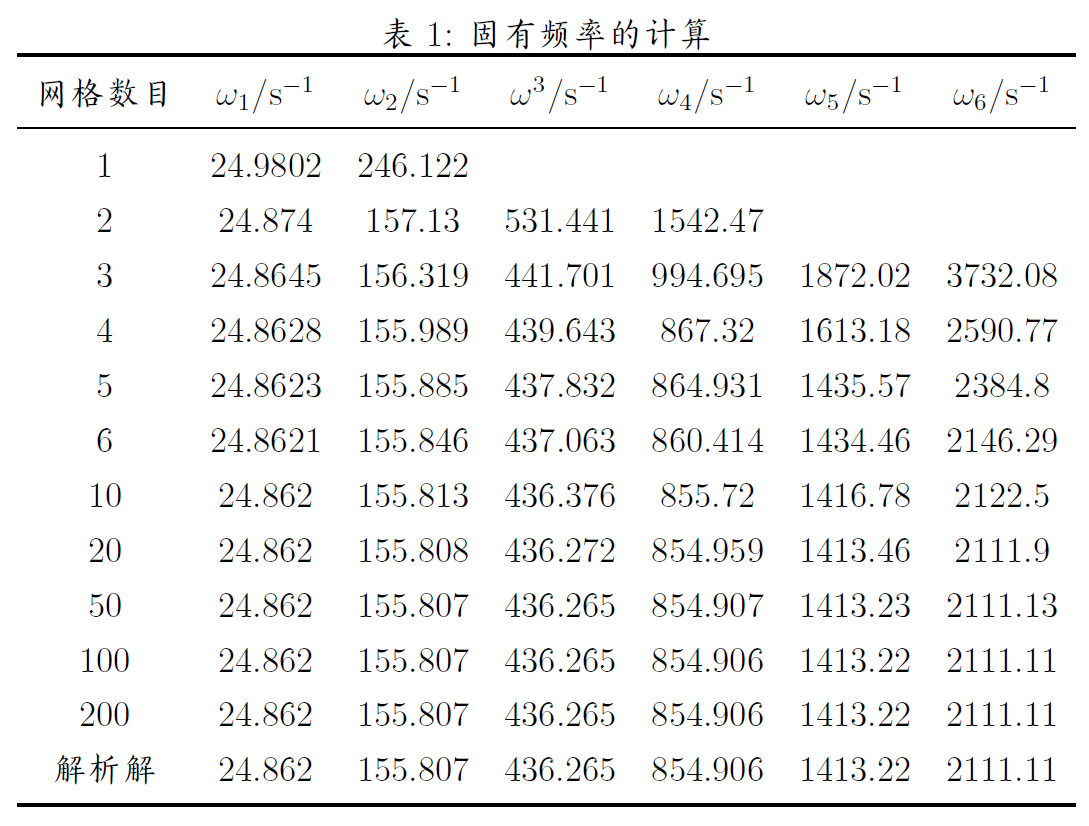
有限元模型计算此模型的固有频率与解析解求得的固有频率对比如表1所示。
龙格库塔算法
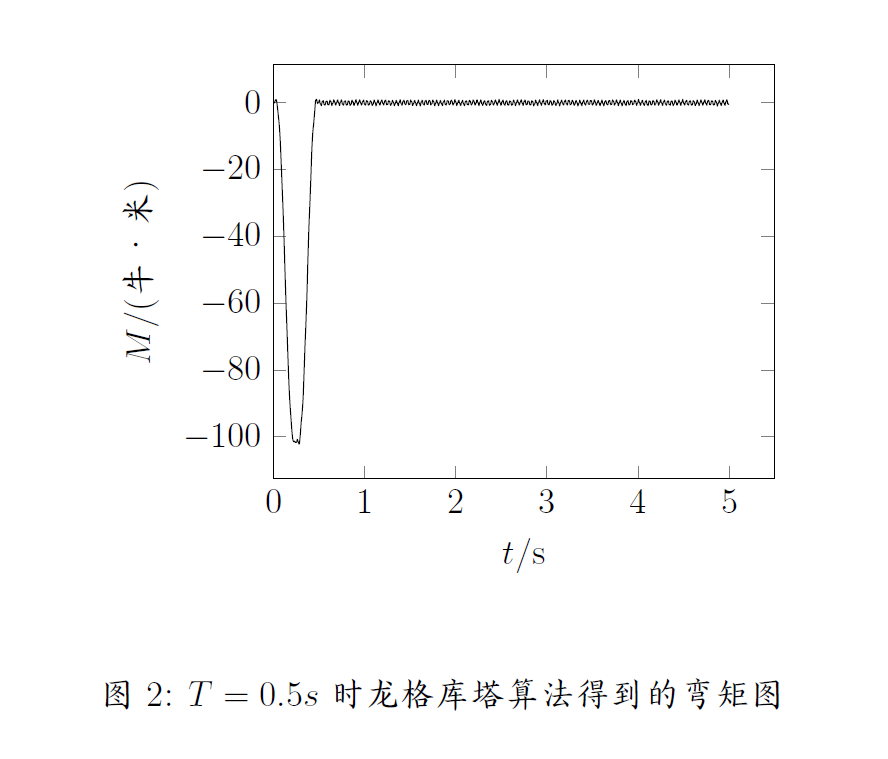
这里采用经典四阶龙格库塔算法。但是由于这里的方程是刚性方程【1】,因此需要将时间步长取到很小才能保证算法的稳定性。在这里得到的结果如图1,图2,图3所示。


韦尔莱积分算法
此系统由于没有黏性项,因此我想到了位置韦尔莱积分会比较方便【2】。即使有速度项也可以用速度韦尔莱积分。
位置韦尔莱的公式以及推导为
\begin{equation} \Rightarrow {\displaystyle r(t+\Delta t)\simeq 2r(t)-r(t-\Delta t)+{\frac {f(t)}{m}}\Delta t^{2}} \end{equation} 新位置的计算误差为四阶。我本以为这样可以让算法能够稳定的,但是发现还是不能取过大的步长。得到的结果由于和龙格库塔得到的结果相同,故略去。
隐式龙格库塔方法
隐式龙格库塔方法可以具有更好的数值稳定性,更适合用于刚性方程的求解。方程如下:
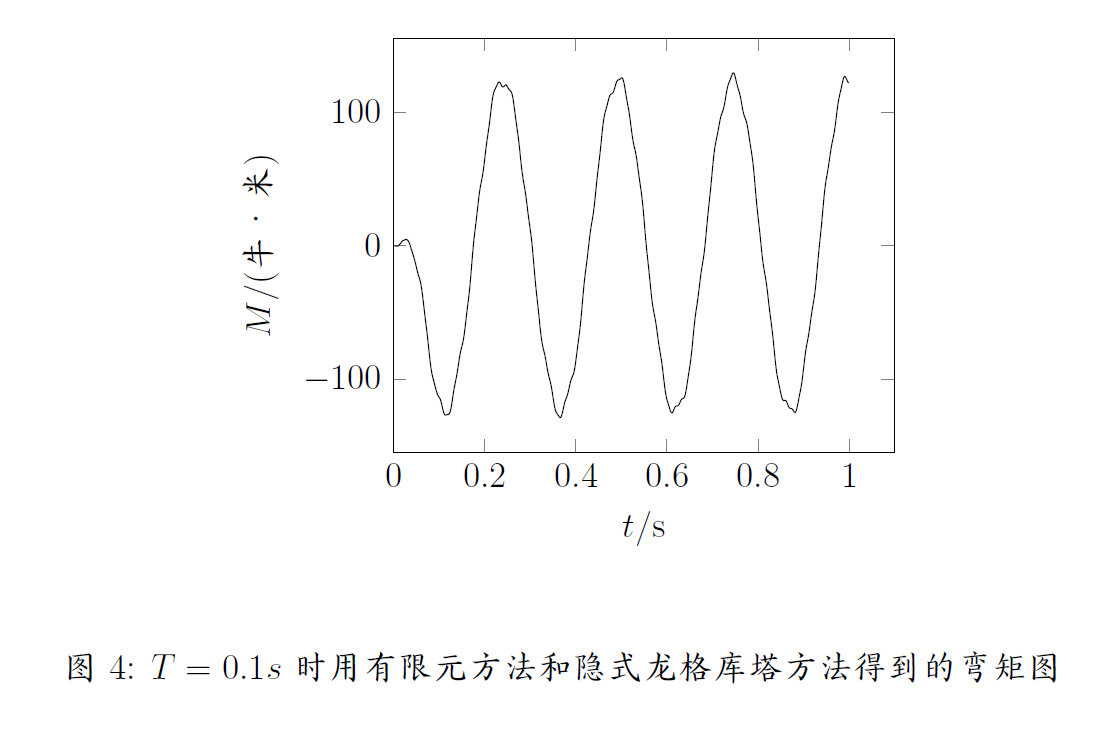
上式中的隐式方程可以用不动点迭代求解。隐式龙格库塔方法可以在更大的时间步长下保证稳定性。得到的结果如图4,图5,图6所示。
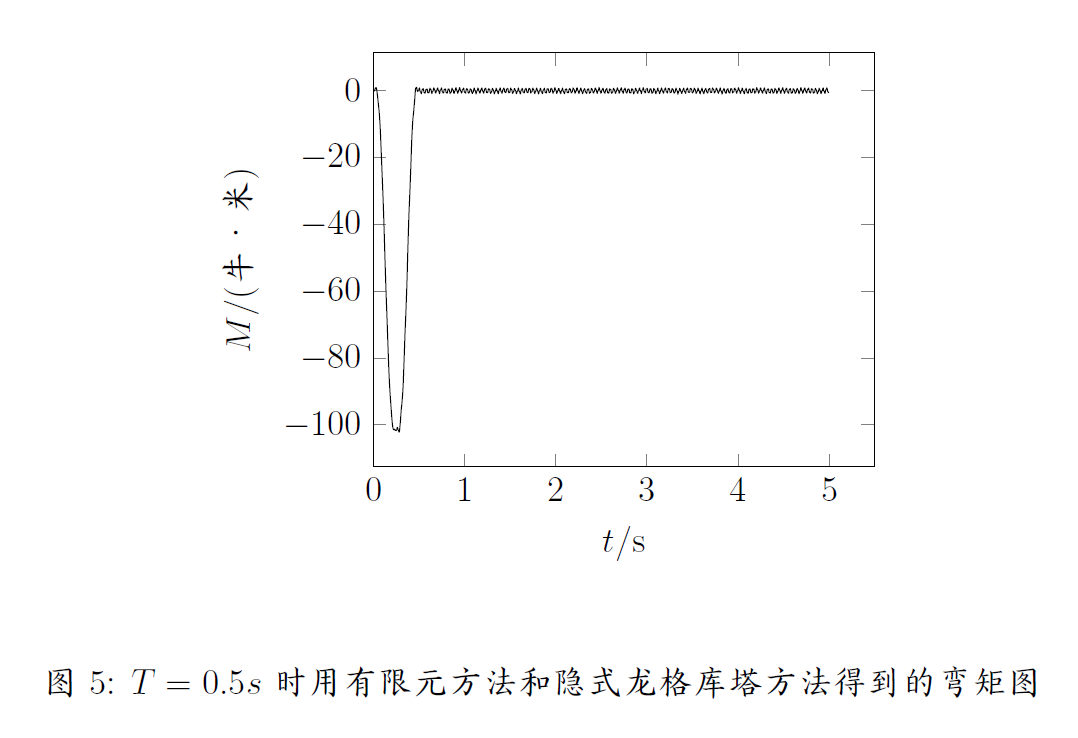
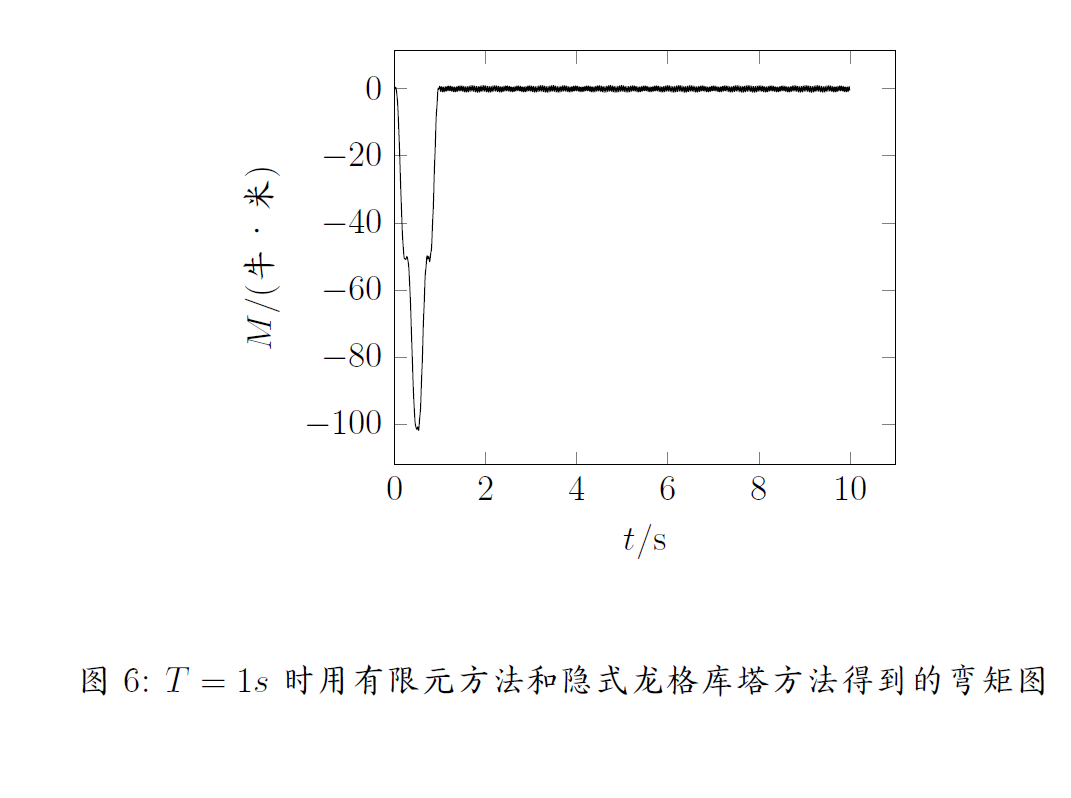
实际上针对刚性方程还有更为有效的算法:Rosenbrock算法【3】,但是由于考前时间有限,没办法去实现了。
Newmark-β方法
根据【4】,一种常用的Newmark方法可以保证无条件稳定:
Newmark方法除了需要初始位移和初始速度以外,还需要初始加速度。且Newmark方法得到的相位误差滞后。得到的结果和前面的结果几乎相同,因此不再重新作图。
时域和频域混合的方法
梁的模态分解及传递函数
梁的受迫振动方程为 \begin{equation}\label{beamMotion} EI\frac{\partial^4u}{\partial x^4}+\rho\pyypxx{u}{x}=f_0\sin\omega t\delta(x-l) \end{equation} 通过分离变量可以得到梁的自由振动下的固有振型和固有频率,分别为$\phi_i,\omega_i$,其中 \begin{equation} \phi_i(x)=\cosh(\alpha_i x)-\cos(\alpha_i x)+\beta_i[\sinh(\alpha_i x)-\sin(\alpha_i x)] \end{equation} 且满足
当梁的自由端作用外力时,按模态进行分解,梁的响应可以设为
\begin{equation}\label{eq1}
u(t)=\sin\omega t\sum c_i\phi_i(x)
\end{equation}
求出不同模态对这个激励的响应,将式(\ref{eq1})代入至式(\ref{beamMotion})中,乘上某个特定的模态,利用正交性,对式子从$0$到$l$积分,并且
\begin{equation}
\int_{a^-}^{a^+}p(x)\delta(x-a)dx=p(a)
\end{equation}
可以得到
\begin{equation}
c_i=\frac{1}{\rho l}\frac{f_0}{\omega_i^2-\omega^2}
\end{equation}
分解模态后用龙格库塔算法
可以利用模态分解后得到的式子列出二阶运动的微分方程,并用龙格库塔算法求解。当$T=0.1s$时,取前两阶模态计算,当$T=0.5s/1s$时,只取系统的基频计算。得到的梁根部弯矩的响应曲线分别如图7,图8,图9所示。对模态分解之后得到的二阶微分方程仍然是刚性方程,为了求解的数值稳定性,龙格库塔方法的计算步长依然需要很小。因此此种方法相对于纯时域方法只是减少了有限元方法的运算量,龙格库塔算法仍需要大量运算。

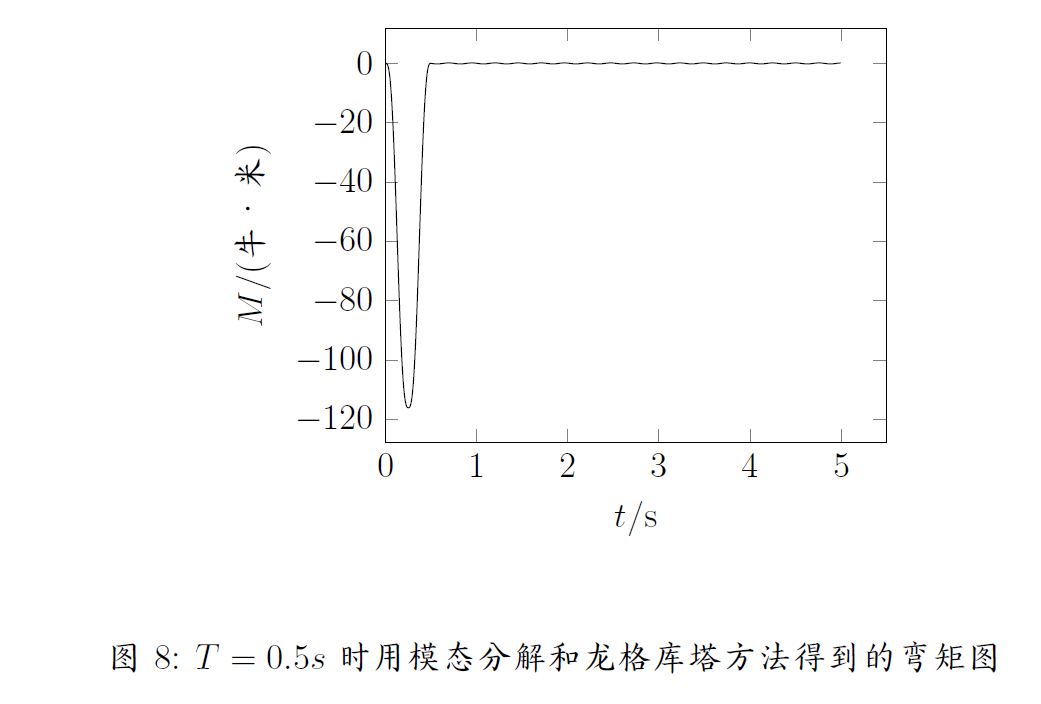

分解模态后用杜哈梅尔积分
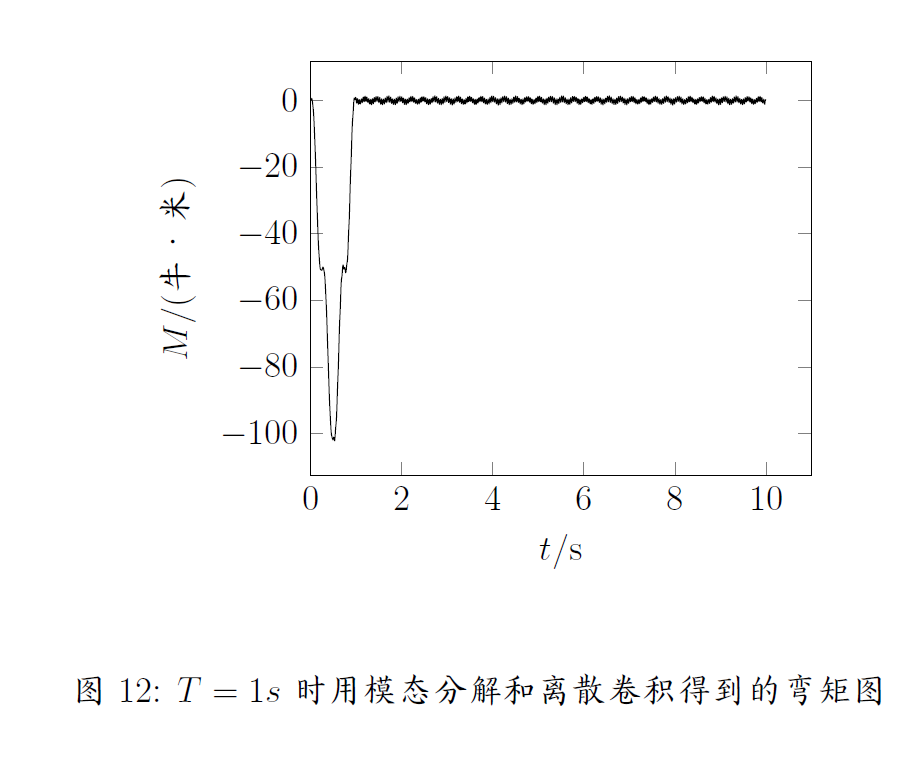
由条件可知,系统的模态为一个无阻尼二阶系统,可以得到系统的单位脉冲响应为 \begin{equation} c(t)=\frac{1}{\rho l\omega_i}\sin(\omega_i t) \end{equation} 将任意载荷$f(t)$视为一系列脉冲激励的迭加: \begin{equation} f(t)\approx \sum {f(\tau )\cdot \Delta \tau \cdot \delta }(t-\tau ) \end{equation} 那么根据线性性质可知,系统的响应同样可以表示成对这一系列脉冲激励的响应函数的迭加: \begin{equation}\label{eq:dis} x(t)\approx \sum {f(\tau )\cdot \Delta \tau \cdot c}(t-\tau ) \end{equation} 根据此编写程序,取前九阶模态,可以得到的响应曲线分别如图10,图11,图12所示。这种方法的运算量相对小很多,而且准确性很高,但是仍然注意到进行离散卷积时采用的取样点的周期如果大于最高阶模态的周期的话会导致很大的误差,因此需要要么少取一些高阶模态,要么减小采样周期。
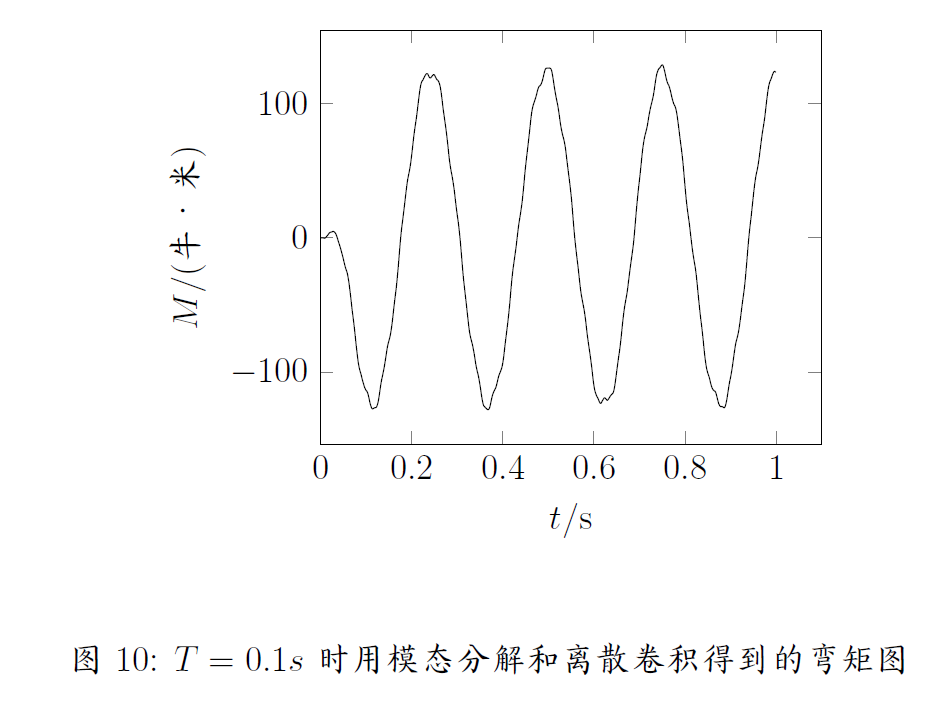

纯时域方法
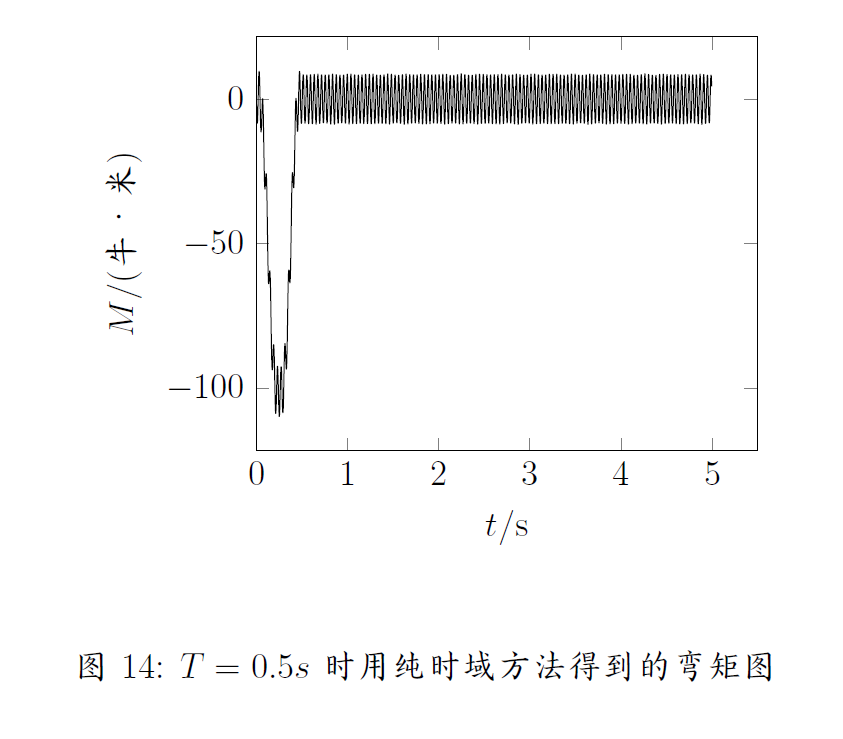
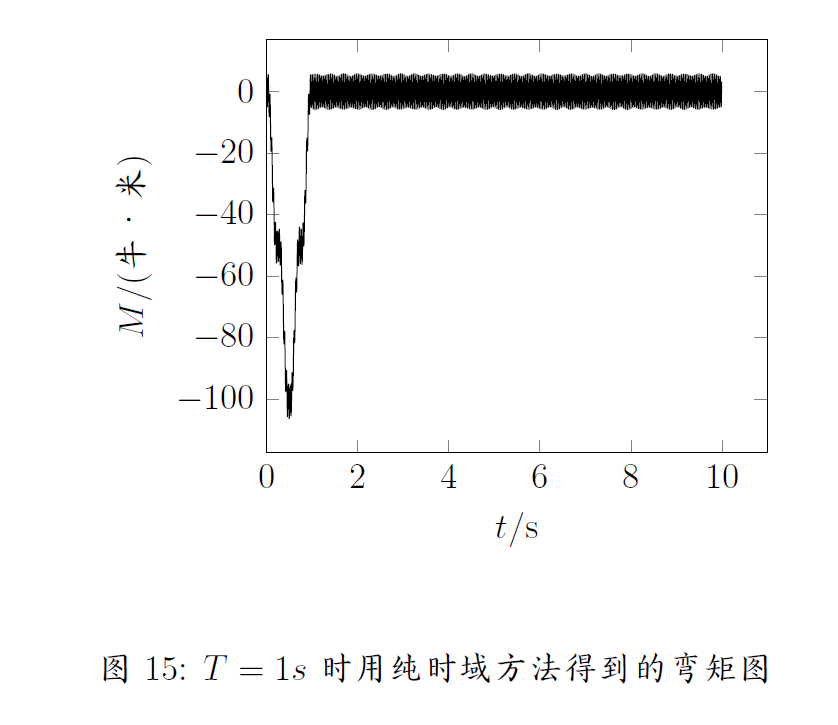
对于题目中给的输入信号,我们可以想通过FFT把他分解成三角函数的和的形式,再分别利用FRF对响应的幅值和相位进行计算,再利用IFFT还原为响应。这种方法的理论基础是卷积定理【5】: \begin{equation} \mathcal{F}(f*g) = \mathcal{F}(f) \cdot \mathcal{F}(g) \end{equation} 可以想象成杜哈梅尔积分的时域形式,单位冲击响应的频域表达式就是FRF.取前七阶模态,这种方法得到的结果分别如图13,图14,图15所示。这种方法的速度很快,这里我自己写的递归FFT并非最快的,如果使用蝶形分治算法还能提升FFT的计算效率。但是这种方法的精度貌似不高,而且和采样周期以及采样时间有很大关系。

参考文献
【1】Ernst Hairer and Gerhard Wanner. Solving Ordinary Differential Equations II. Stiff and Differential-Algebraic Problems. Springer, Berlin, 1996. ID: unige:12344.
【2】Jason Gregory. Game engine architecture. Taylor & Francis Ltd., 1 edition, 2009.
【3】William H. Press, Saul A. Teukolsky, William T. Vetterling, and Brian P. Flannery. Numerical Recipes 3rd Edition: The Art of Scientific Computing. Cambridge University Press, New York, NY, USA, 3 edition, 2007.
【4】邢誉峰,李敏. 计算固体力学原理与方法. 北京航空航天大学出版社, 2011.
【5】Albert Boggess and Francis J Narcowich. A First Course in Wavelets with Fourier Analysis. Publishing House of Electronics Industry, 2002.