It is natural to look forward to those discrete systems which preserve as much as possible the intrinsic properties of the continuous system. (Feng Kang 1985)
哈密顿系统与刘维尔定理
哈密顿系统通常可以写成这样的形式:
其中$p$为广义动量,$q$为广义坐标(这里为了简化没有写成向量的黑体)。
假设哈密顿系统是可分离的,也就是说,哈密顿函数可以写成下面的形式 \begin{equation} H(p,q)=T(p)+V(q) \end{equation} 这个是可以在大部分的哈密顿系统中满足,其中$T$就是动能,而$V$就是势能。
刘维尔定理:哈密顿系统的相流保持相体积不变。要证明刘维尔定理,只需要证明常微分方程组的散度为0,而这个是易证的。具体证明过程可以参考阿诺尔德的教材《经典力学的数学方法》,这里就不给出详细的证明过程了。那么我们还可以得到结论:哈密顿方程组在相空间中不可能有渐进稳定的点和渐进稳定的极限环。由刘维尔定理还可以推出庞加莱回归定理,具体表述也可以参考阿诺尔德的教材。
数值积分算法
我之前的讨论讨论了许多常用的积分算法,但是这些算法对于哈密顿系统而言有一个缺点:并不保辛。可以用一个直观的图片来反应这个现象:
 像这样的一个哈密顿系统,起初在相流当中有一个图形,根据刘维尔定理经过变换后的图形的面积应该和原图形相等,然而欧拉算法、龙格库塔算法却没有出现这样的现象,因此我们需要保辛的算法。
像这样的一个哈密顿系统,起初在相流当中有一个图形,根据刘维尔定理经过变换后的图形的面积应该和原图形相等,然而欧拉算法、龙格库塔算法却没有出现这样的现象,因此我们需要保辛的算法。
分块龙格库塔算法
对于哈密顿方程,可以使用分块的龙格库塔算法: \begin{equation} P_i=p_0+h\sum_j a_{ij}k_j\quad Q_i=q_0h\sum_j \hat a_{ij}l_j \end{equation} \begin{equation} p_1=p_0+h\sum_i b_ik_i\quad q_1=q_0+h\sum_i \hat b_il_i \end{equation} \begin{equation} k_i=-\pypx{H}{Q}{P_i,Q_i}\quad l_i=\pypx{H}{p}(P_i,Q_i) \end{equation} 对于分块龙格库塔算法,有如下定理:如果上式中的系数满足: \begin{equation} b_i=\hat{b_i} \end{equation} \begin{equation}\label{cond1} b_i\hat a_{ij}+\hat b_j a_{ji}-b_i\hat b_j=0 \end{equation} 那么算法是保辛的。进一步,若哈密顿系统是可分离的,那么如果系数满足式(\ref{cond1})就说明算法是保辛的。因此,我们可以将系数用如下方式简化:
并令
则可以满足式(\ref{cond1}),直观的可以写成表格:
 算法形式:
算法形式:
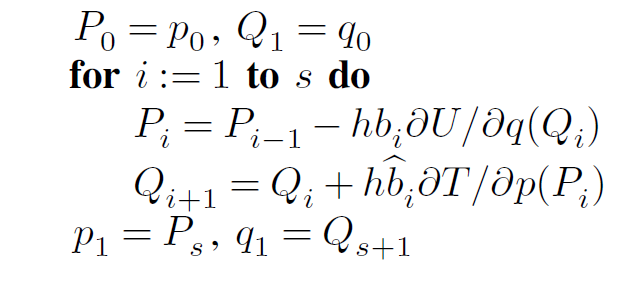
特殊情况是当$s=1$时,有分块欧拉方法 \begin{equation} p_1=p_0-h\pypx{U}{q}(q_0)\quad q_1=q_0+h\pypx{T}{p}(p_1) \end{equation} 交换$p,q$还可以得到 \begin{equation} q_1=q_0+h\pypx{T}{p}(p_0)\quad p_1=p_0-h\pypx{U}{q}(q_1) \end{equation} 上面两种算法是保辛且互为伴随的。
三阶的系数可以取
四阶的系数可以取
参考文献
【1】Symplectic integrator - Wikipedia感觉好像有地方有错
【2】Ernst Hairer, Syvert P. Nørsett, and Gerhard Wanner, Solving Ordinary Differential Equations I: Nonstiff Problems, 2nd ed. (Springer, Berlin, 2009).
【3】B.И.阿诺尔德, 阿诺尔德, 齐民友. 经典力学的数学方法[M]. 高等教育出版社, 2006.
【4】Haruo Yoshida, “Construction of higher order symplectic integrators,” Physics Letters A 150, no. 5 (November 12, 1990): 262-268.
【5】Forest, E.; Ruth, Ronald D. (1990). “Fourth-order symplectic integration”. Physica D. 43: 105.