探讨牛顿平方反比定律与胡克定律的对偶性,研究相关的动力学系统以及共形映射。本文的大多数结论来自于Arnold等人的著作。
本文公式较多,在浏览器中将会花较长时间用于渲染公式。
共形映射
这个是复变函数论的一个重要工具,在这里我们需要以下两个共形映射函数。(吐槽一下,百度的ECharts实在不适合绘制数学函数)
茹科夫斯基函数
\begin{equation}
f(z) = z+\frac{1}{z}
\end{equation}
若$z=|R|>1$,则得到的是焦点为$\pm 2$的椭圆,证明如下:
\begin{equation}
z=R(\cos\theta+i\sin\theta)
\end{equation}
那么有
很显然可以得到:
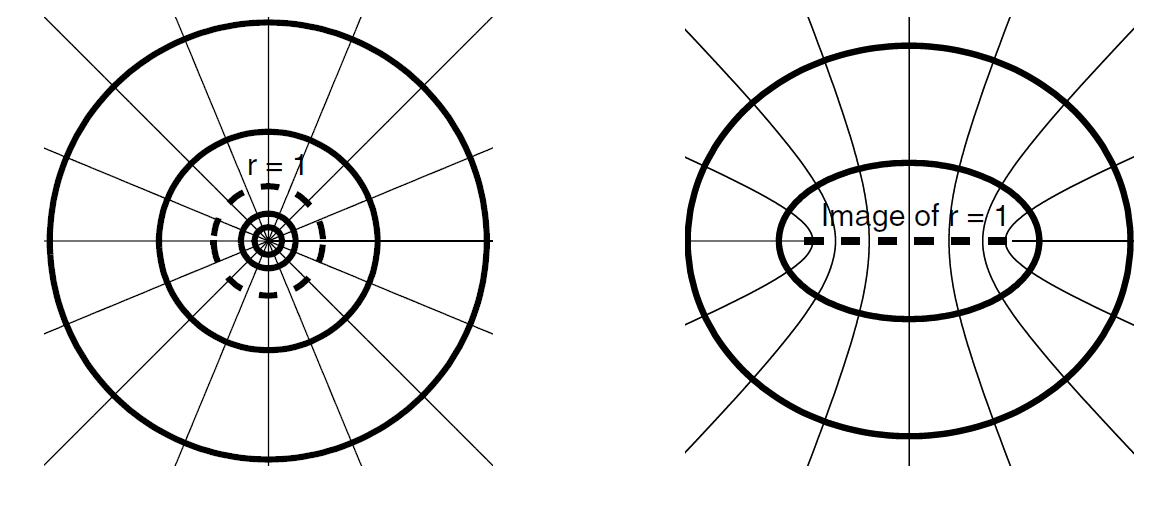
平方函数
\begin{equation}
f(z)=z^2
\end{equation}
设$z$为一个椭圆,$z=a\cos\theta+ib\sin\theta$
则有:
可以得到映射后的图形是其中一个焦点在原点的椭圆
胡克定律
胡克定律
\begin{equation}
\mathbf{F}=-k\mathbf{x}
\end{equation}
这个东西与椭圆也大有关系。首先,在一维问题中,如果一个小球和弹簧相连,那么会形成简谐振动,而简谐振动的相平面就是椭圆(能量守恒易得)。我们考虑更加复杂的情况:一个弹簧连着一个小球进行二维平面运动,也会得到椭圆的运动轨迹,证明如下[1]:
将平面运动分解为径向和周向的速度分量,角动量方程为:
\begin{equation}
L=mr^2\dot\theta
\end{equation}
能量方程为:
\begin{equation}
E=\frac{1}{2}m\dot r^2+\frac{L^2}{2mr^2}+U(r)
\end{equation}
根据以上两个方程,可以分别求出$r,\theta$对时间的导数,因此可以得到
\begin{equation}
\frac{dr}{d\theta}=\frac{dr/dt}{d\theta/dt}=\pm\sqrt{\frac{2m}{l^2}}r^2\sqrt{E-l^2/2mr^2-U(r)}
\end{equation}
\begin{equation}
\theta=\int d\theta=\pm\frac{l}{\sqrt{2m}}\int^r\frac{dr/r^2}{\sqrt{E-l^2/2mr^2-U(r)}}
\end{equation}
势能的表达式
\begin{equation}
U=0.5kr^2
\end{equation}
因此可以得到
\begin{equation}
\theta(r)=\pm\frac{i}{\sqrt{2m}}\int^r\frac{dr/r^2}{\sqrt{E-l^2/2mr^2-0.5kr^2}}
\end{equation}
令$z=r^2$,有
\begin{equation}
\theta(z)=\pm\frac{l}{2\sqrt{2m}}\int^z\frac{dz/z}{\sqrt{-l^2/2m+Ez-(k/2)z^2}}
\end{equation}
因为
\begin{equation}
\int^z\frac{dz/z}{\sqrt{a+bz+cz^2}}=\frac{1}{-a}\mathrm{asin}(\frac{bz+2a}{z\sqrt{b^2-4ac}})
\end{equation}
所以有
\begin{equation}
\theta-\theta_0=\pm\frac{1}{2}\mathrm{asin}(\frac{Er^2-l^2/m}{r^2\sqrt{E^2-kl^2/m}})
\end{equation}
反解$r$得到
\begin{equation}
r^2(\theta)=\frac{l^2/m}{E\mp(\sqrt{E^2-kl^2/m})\sin{2(\theta-\theta_0)}}
\end{equation}
显然,这个轨道是闭合的(因为$r^2(\theta+2\pi)=r^2(\theta)$),也可以证明表示的是一个椭圆(把分母有理化)。不过如果我们知道比如长轴的位置速度信息,求短轴就不必这么麻烦,一个角动量守恒方程一个能量守恒方程就可以得到短轴的位置速度。
牛顿平方反比定律与胡克定律的对偶性
参考文献为[2](W. Hall, Rachel & Josic, Kresimir. (2000). Planetary Motion and the Duality of Force Laws. Society for Industrial and Applied Mathematics. 42. 115-124. 10.1137/S0036144598346005. )
考虑胡克定律的动力学形式为复数形式:
\begin{equation}
\ddot w = -Cw
\end{equation}
这里的时间自变量为$t$,假设另一个时间变量$\tau$满足$\tau=\tau(t)$,另外一个运动$z=z(\tau)$,我们会得到$\frac{d^2z}{d\tau^2}=-\tilde{C}\frac{z}{|z|^3}$.
事实上,只要做变换$z=w^2$,并令$\frac{d\tau}{dt}=|w|^2$,就可以得到平方反比的形式,证明如下:
现在令$E_w=\frac{1}{2}(|\dot w|^2+C|w|^2)$,可以得到
\begin{equation}
\frac{d^2 z}{d\tau^2}=-4E_ww^{-1}\bar w^{-3}=-4E_w\frac{z}{|z|^3}
\end{equation}
这就是我们想要得到的形式。不得不说,Arnold等人的想法太意识流了,这也能想到。
其实核心就在于上面的那个平方关系的共形映射,让中心在原点的椭圆映射到焦点在原点的椭圆。而那个$\tau,t$的关系是如何得到的呢?事实上,由于角动量守恒,胡克椭圆和开普勒椭圆都会满足面积率。我们记$A_1,A_2$分别是$w(t),z(\tau)$所扫过的面积。$w(t)=(r,\theta)$,而$z=w^2(t)=(r^2,2\theta)$.可以得到
这样想到的取$\frac{d\tau}{dt}=|w|^2$……
上面这个东西还可以进一步推论:点在幂为$a$的力场中的轨道,在经过适当的变换$w=z^\beta$后变成幂为A的力场中的轨道,则有$A,a,\beta$满足:
证明过程与刚才类似,不过需要注意的是要选择的$\tau$要满足关系
\begin{equation}
\frac{d\tau}{dt}=\frac{|z(\tau(t))|^2}{|w(t)|^2}=|w(t)|^{2(\beta-1)}
\end{equation}