申伟宏
设梁单元的形函数为多项式，并由卡氏第一定理可以推导弯曲单元刚度矩阵 \begin{equation}\label{k_bending_unit} [k_e]=\frac{EI_Z}{L^3}\begin{bmatrix} 12 & 6L & -12 & 6L \\ 6L & 4L^2 & -6L & 2L^2 \\ -12 & -6L & 12 & -6L \\ 6L & 2L^2 & -6L & 4L^2 \end{bmatrix} \end{equation} 单个具有弯曲和扭转的单元的刚度矩阵为（这里假定梁为圆柱形截面） \begin{equation} \begin{bmatrix} [k_\text{bending}]_{xy} & [0] \\ [0] & [k_\text{torsion}] \end{bmatrix} \begin{bmatrix} \nu_1 \\ \theta_{z1} \\ \nu_2 \\ \theta_{z2} \\ \theta_{x1} \\ \theta_{x2} \end{bmatrix} = \begin{bmatrix} f_{y1} \\ M_{z1} \\ f_{y2} \\ M_{z2} \\ M_{x1} \\ M_{x2} \end{bmatrix} \end{equation}
扭转子刚度矩阵为 \begin{equation} [k_\text{torsion}]=\frac{JG}{L} \begin{bmatrix} 1 & -1 \\ -1 & 1 \end{bmatrix} \end{equation} 而扭转产生的切应力计算公式为： \begin{equation} \tau = G\gamma =G\rho \dydx{\varphi}{x} = G\rho\frac{M}{GI_p} \end{equation}
有限元方程得到的矩阵通常是稀疏矩阵，通常用专门的稀疏矩阵算法对矩阵进行存储和计算。常见的适合用于解决这方面问题的程序库包括Eigen和deal.II.对于线性方程 \begin{equation}\label{fem_basic} \bm{Ku-f=0} \end{equation} 当问题的自由度相对较小时，可以采用LU分解或者Cholesky分解的方式。Cholesky分解在这类问题中得到广泛运用：对正定埃尔米特矩阵$\bm{A}$进行Cholesky分解，即求 矩阵$\bm{L}$使得下式成立： \begin{equation} \bm{A=LL}^* \end{equation} 式中，$\bm{L}$为一个下三角矩阵且所有对角元素均为正实数，$\bm{L}^*$为$\bm{L}$的共轭转置矩阵。当$\bm{A}$是正定矩阵时，Cholesky分解是惟一的。 Cholesky分解的另一种形式——LDLT分解的计算方式如下所示： \begin{equation} {\displaystyle {\begin{aligned} {\mathbf {A=LDL} ^{\mathrm {T} }}&={\begin{pmatrix} 1&0&0\\L_{21}&1&0\\L_{31}&L_{32}&1\\\end{pmatrix}} {\begin{pmatrix}D_{1}&0&0\\0&D_{2}&0\\0&0&D_{3}\\\end{pmatrix}} {\begin{pmatrix}1&L_{21}&L_{31}\\0&1&L_{32}\\0&0&1\\\end{pmatrix}} \\&={\begin{pmatrix}D_{1}&&(\mathrm {symmetric} )\\L_{21}D_{1}&L_{21}^{2}D_{1}+D_{2}&\\L_{31}D_{1}&L_{31}L_{21}D_{1}+L_{32}D_{2}&L_{31}^{2}D_{1}+L_{32}^{2}D_{2}+D_{3}\end{pmatrix}} \end{aligned}}} \end{equation}
| Decomposition | Requirements
on the matrix |
Speed
(small-to-medium) |
Speed
(large) |
Accuracy |
|---|---|---|---|---|
| PartialPivLU | Invertible | ++ | ++ | + |
| FullPivLU | None | - | - - | +++ |
| HouseholderQR | None | ++ | ++ | + |
| ColPivHouseholderQR | None | + | - | +++ |
| FullPivHouseholderQR | None | - | - - | +++ |
| CompleteOrthogonalDecomposition | None | + | - | +++ |
| LLT | Positive definite | +++ | +++ | + |
| LDLT | Positive or negative
semidefinite |
+++ | + | ++ |
| BDCSVD | None | - | - | +++ |
| JacobiSVD | None | - | - - - | +++ |
例如，对于稀疏矩阵的线性方程组求解，一般采用迭代的算法进行求解。对于自伴随矩阵 ，可以采用共轭梯度下降法求解，而对于一般的方阵则采用BiCGStab算法求解。对于大规模稀疏线性方程组，迭代算法能够比矩阵分解算法更高效。
在我的有限元程序里面使用LDLT分解求解有限元方程。
片条理论是一种忽略了下洗的计算方法，能够简单快捷地计算升力分布。在机翼的展弦比大于5的时候，能够给出足够精确的结果。将机翼分成若干个片条，各个片条的升力为 \begin{equation} L_i = C_L^\alpha \alpha_iS_i \end{equation} 在这里升力线斜率需要用经验公式修正。在处理静气动弹性问题时，由于翼面的扭转变形，攻角沿翼展变化，这时可以用一个修正公式 \begin{equation} \pypx{C_L}{\alpha} = (\pypx{C_L}{\alpha})_\infty \frac{\lambda}{\lambda + 4} \end{equation} 通常处理气动力计算时，会引入气动力影响矩阵$\bm{A}$，片条理论的气动力影响矩阵为 \begin{equation} \bm{A} = \text{diag}[\frac{1}{C_L^\alpha c_i}\quad\cdots\quad\frac{1}{C_L^\alpha c_n}] \end{equation} 式中，$C_L^\alpha$应按风洞试验结果或按理论公式计算，$c$为弦长。 那么攻角与升力系数满足以下关系 \begin{equation} \bm{As}=\bm{\alpha} \end{equation}
由于片条理论忽略了下洗，因此会导致气动力计算的不准确，并且无法计算诱导阻力。经典的升力线方法考虑翼型的升力系数随攻角线性变化，并且不考虑气体的粘性。
普朗特升力线理论的基本方程 \begin{equation}\label{eqs:llt} \alpha(y_0)=\frac{\Gamma(y_0)}{\pi V_\infty c(y_0)}+\alpha_0+\frac{1}{4\pi}\int_{-b/2}^{b/2}\frac{(d\Gamma/dy)dy}{y_0-y} \end{equation} 而诱导阻力的公式为 \begin{equation} D_i^\prime=L_i^\prime \sin\alpha_i\approx L_i^\prime \alpha_i \end{equation} \begin{equation} D_i=\rho_\infty V_\infty\int_{-b/2}^{b/2}\Gamma(y)\alpha_i(y)dy \end{equation} 通过对上式进行离散化处理，采用数值积分的方式，并进行迭代计算环量$\Gamma(y)$的分布，可以在计算机上对方程（\ref{eqs:llt}）进行数值求解。
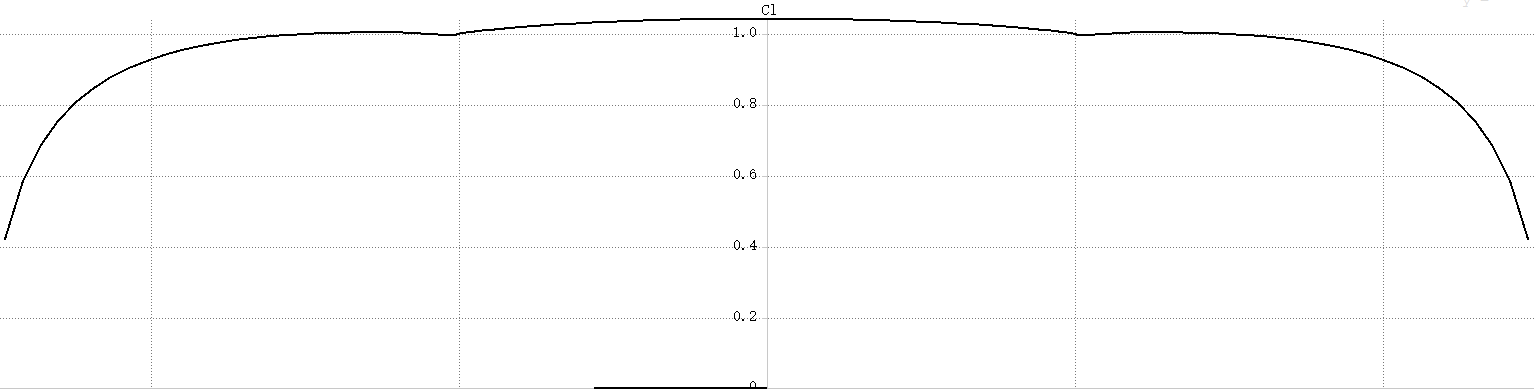
由于针对CFD求解机翼流场的成本巨大，因此工程上常常采用涡格法求解机翼流场。涡格法在面元上布置点源、点涡或者偶极子，通过控制点法向速度为0的边界条件，可以比较精确得解出下洗、诱导阻力、升力等。在势流理论中，的一个基本解是源（汇）。当这个元素的强度是正的时候，就被称为源，负的称为汇。在$(x_0,y_0,z_0)$的源作用在位于点$P(x,y,z)$ 的点的速度势为 \begin{align} \phi(P(x,y,z)) &=-\frac{\sigma}{4\pi|\bm{r}-\bm{r}_0|} \quad & \text{(球坐标)} \notag\\ &= \frac{-\sigma}{4\pi\sqrt{(x-x_0)^2+(y-y_0)^2+(z-z_0)^2}} \quad &\text{(直角坐标)}\label{eqs2_17} \end{align} 可以将基本解分布在表面上，通常称为板块或者面元。因此分布在某个面上的源作用在点$P(x,y,z)$的速度势能够通过积分式(\ref{eqs2_17})得到 \begin{equation}\label{eqs2_18} \phi(P(x,y,z))=\frac{-1}{4\pi}\int_S\frac{-\sigma(x_0,y_0,z_0)}{(x-x_0)^2+(y-y_0)^2+(z-z_0)^2}dS \end{equation} 而若在表面布置偶极子或者点涡，则可以得到环量并计算升力。由涡格法可以得到方程： \begin{equation}\label{eqs_vlm} \bm{A\Gamma=v} \end{equation} 其中$\bm{A}$是气动力影响系数矩阵，$\bm{\Gamma}$是各个面元的环量组成的向量，$\bm{v}$是边界条件向量，也就是各个面元的当地攻角。
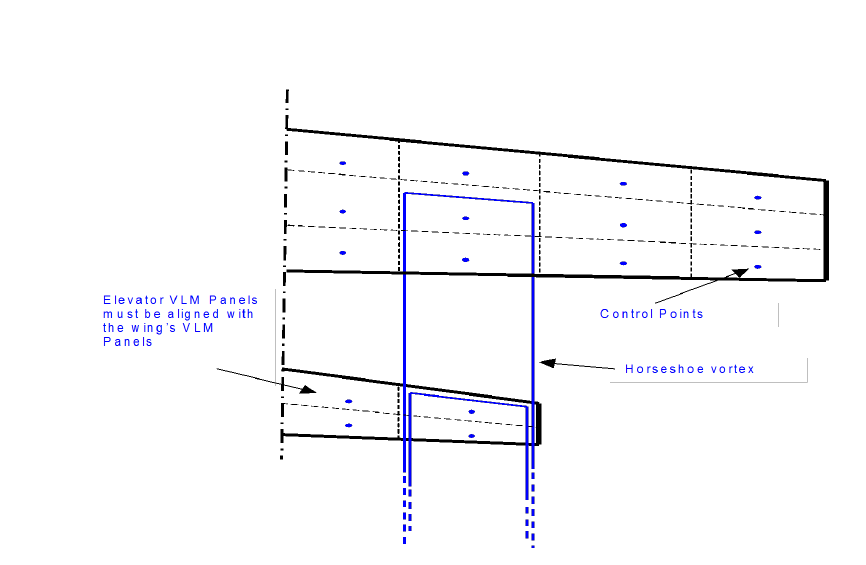
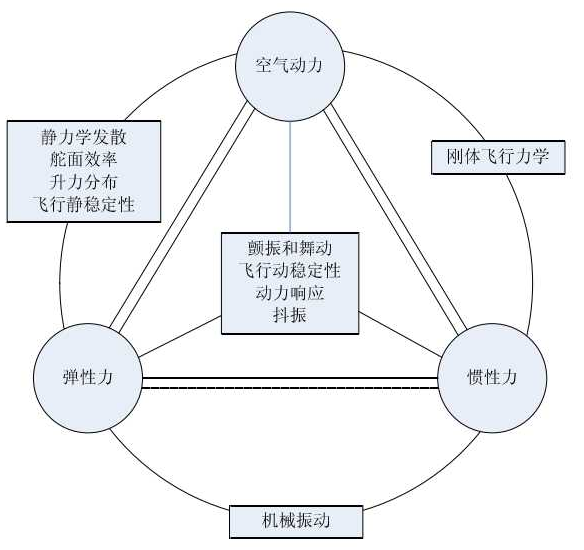
“气动弹性力学”概念最早由航空工程师在20世纪30年代引出，到现在已经发展成为了一门独立的力学学科，其主要考虑气动力与弹性体之间的相互作用，进而研究弹性结构在气流中的力学行为。气流中的弹性结构在空气动力的作用下回发生弹性变形或振动，而结构变形又会让气动力重新分布，这种结构与气动间的相互耦合作用使弹性体产生各类气动弹性现象。为了明确气动弹性力学的分类以及了解气动弹性问题的研究内容，英国学者Collar在1946年绘制了气动弹性力学三角形，生动具体地表示了气动弹性力学所涉及的各个学科以及各学科间的相互联系，如图所示。
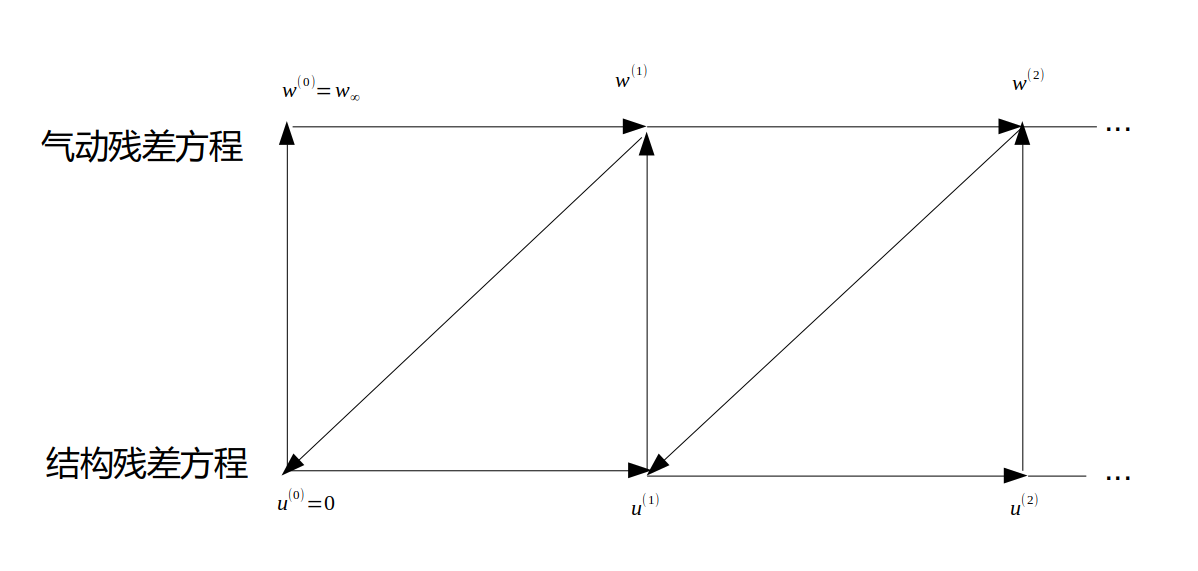
流体力学残差方程为 \begin{equation}\label{femResidual} \bm{R = Aw - \alpha = 0} \end{equation} 有限元残差方程为 \begin{equation}\label{aeroResidual} \bm{S = Ku-f=0} \end{equation} 气动弹性力学的求解器通过耦合结构的有限元方程和气动的气动力方程，在收敛求解的过程中，通过分别求解结构残差方程式(\ref{femResidual})和气动残差方程(\ref{aeroResidual})，并互相使用求解出的气动力和位移数据，不断迭代，直到收敛。在这里我们仅仅考虑静气动弹性问题，因此忽略动力学相关的如模态频率，时间步长等因素。
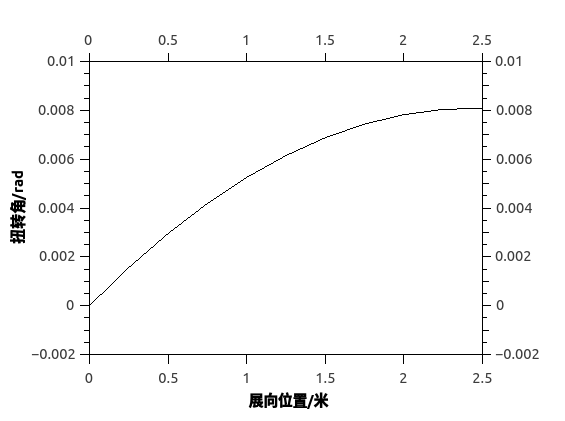
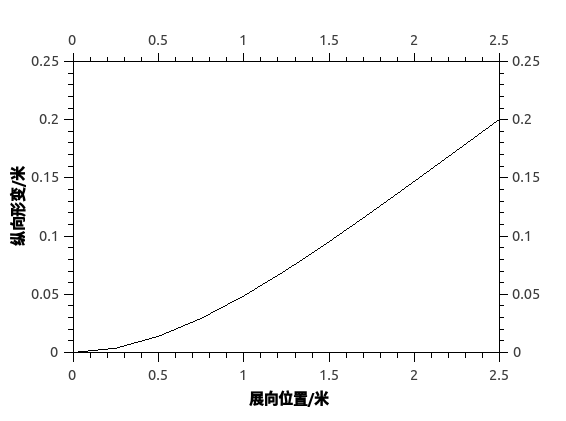
设某段矩形机翼翼展为5米，展弦比为9，机翼梁的为圆柱形实心梁，梁的直径为6cm，梁的材料的弹性模量为2GPa，泊松比为0.2，梁位于弦长的30%处。假设空气密度为$\rho = 1.225\text{kg}/\text{m}^2$,风速为18m/s，机翼对气流的攻角为$5^{\circ}$，机翼的升力线斜率为$5/\text{rad}$.
考虑一个解析函数$F(z)$，这意味着该函数无限可微且能够在光滑的延拓的复平面上，那么对于实数$x_0$和$h$，根据泰勒级数有 \begin{equation} F(x_o+ih)=F(x_0)+ihF(x_0)-\frac{h^2F(x_0)}{2!}\cdots \end{equation} 取虚部可以得到 \begin{equation} F(x_0+ih) = \frac{\mathrm{Im}(F(x_0+ih)}{h}+)(h^2) \end{equation} 因此得到 \begin{equation} F^\prime(x_0)=\frac{\mathrm{Im}(F(x_0+ih))}{h} \end{equation}
自动微分是算导数的最优方法，比符号计算、有限微分更快更精确。自动微 分已经广泛应用在优化领域，包括人工神经网络的训练算法 back-propagation。要解连续优化或非线性方程，自动微分是不二的选择。自动微分的原理即为在函数的每 一次运算中，利用链导法则对每一次运算进行微分。自动微分将符号微分法应用于最基本的算子，比如常数，幂函数，指数函数，对数函数，三角函数等，然后代入数 值，保留中间结果，最后再应用于整个函数。因此它应用相当灵活，可以做到完全向用户隐藏微分求解过程，由于它只对基本函数或常数运用符号微分法则，所以它可以 灵活结合编程语言的循环结构，条件结构等。自动微分可以分为正序模式与倒序模式。正序模式中导数沿着代码的执行路径传播，倒序模式则是要求从输出到输入节点， 按照先后依赖关系，对各个节点求取输出对于当前节点的梯度，一旦搜集好对应输出边节点关于当前节点导数，那么当前节点的导数便可以由链导法则计算得出。通常使 用的方式是倒序模式，因为许多微分过程需要倒序模式才能高效求解。
假设列向量$\bm{x}$是线性方程组$\bm{Ax}=\bm{b}$的解，其中$\bm{A}$是关于设计变量$\bm{p}$的$M\times M$的实数矩阵，$\bm{b}$是关于设计变量$\bm{p}$的实数列向量。为了直接得到$g$的梯度，有 \begin{equation} \frac{dg}{d\bm{p}}=\frac{\partial g}{\partial \bm{p}} + \frac{\partial g}{\partial \bm{x}}\frac{\partial \bm{x}}{\partial \bm{p}}\end{equation} 由于$g$是一个给定的函数，假设$\frac{\partial g}{\partial \bm{p}}$,$\frac{\partial g}{\partial \bm{x}}$不难求得。另一方面，$\frac{\partial \bm{x}}{\partial \bm{p}}$的计算会很困难，因为对于每一个设计变量$p_i$，需要计算$\frac{\partial \bm{x}}{\partial p_i}=\bm{A}^{-1}(\frac{\partial \bm{b}}{\partial p_i}-\frac{\partial \bm{A}}{\partial p_i}\bm{x})$.也就是说，我们需要求解$p$次$M$阶矩阵线性方程，这对于$p,m$特别大的时候是不现实的。 我们可以将问题这样解决： \begin{equation} \pypx{g}{\bm{x}}\frac{\partial \bm{x}}{\partial \bm{p}}=\frac{\partial g}{\partial \bm{x}}[\bm{A}^{-1}(\frac{\partial \bm{b}}{\partial \bm{p}}-\frac{\partial \bm{A}}{\partial \bm{p}}\bm{x})]=[\frac{\partial g}{\partial \bm{x}}\bm{A}^{-1}](\frac{\partial \bm{b}}{\partial \bm{p}}-\frac{\partial \bm{A}}{\partial \bm{p}}\bm{x})\end{equation} 并令 \begin{equation}\label{eqs_adj} \bm{A}^T \bm{\lambda}=\frac{\partial g}{\partial \bm{x}}^T\end{equation} 则可以得到： \begin{equation} \frac{dg}{d\bm{p}}=\frac{\partial g}{\partial \bm{p}} - \bm{\lambda}^T(\frac{\partial \bm{b}}{\partial \bm{p}}-\frac{\partial \bm{A}}{\partial \bm{p}}\bm{x})\end{equation} 通过伴随方法，这样可以只求解一次$p$次$M$阶矩阵线性方程式（\ref{eqs_adj}）。 在这里$\pypx{\bm{A}}{\bm{p}}$是三阶张量。
有限元的基本方程可以写为式(\ref{femResidual})的形式， 由于在这里仅仅考虑静载荷问题，因此有$\pypx{\bm{f}}{\bm{p}}=0,\pypx{\bm{f}}{\bm{u}}=0$，因此有 \begin{equation} \bm{K}\delta u=-\pypx{\bm{K}}{\bm{p}}\bm{u}\delta\bm{p} \end{equation} 记$I$为性能指标，约束方程为 \begin{equation} R(\bm{u,f,p})=\bm{Ku-f}=0 \end{equation} \begin{equation} \delta I={\pypx{I}{\bm{u}}}^T\delta\bm{u}+\pypx{I}{\bm{f}}\delta\bm{f}+\pypx{I}{\bm{p}}\delta{\bm{p}} \end{equation} \begin{equation} \delta{R}=\pypx{\bm{R}}{\bm{u}}\delta\bm{u}+\pypx{\bm{R}}{\bm{f}}\delta\bm{f}+\pypx{\bm{R}}{\bm{p}}\delta{\bm{p}} \end{equation} 这就可以看做是一个带约束的优化问题。带约束的优化问题通常可以使用拉格朗日乘数法则。设伴随向量为$\bm{\psi}$，也可以看作拉格朗日乘子。用拉格朗日乘数法则可以得到 \begin{equation} \delta I=[\pypx{I^T}{\bm{u}}-\bm{\psi^T}\pypx{\bm{R}}{\bm{u}}]\delta\bm{u}+[\pypx{I^T}{\bm{f}}-\bm{\psi^T}\pypx{\bm{R}}{\bm{f}}]\delta\bm{f}+[\pypx{I^T}{\bm{p}}-\bm{\psi^T}\pypx{\bm{R}}{\bm{p}}]\delta\bm{p} \end{equation}
选择伴随向量$\bm{\psi}$满足 \begin{equation} (\pypx{\bm{R}}{\bm{u}})^T\bm{\psi}=\pypx{I}{\bm{u}} \end{equation} 且记$$\bm{G_f}=\pypx{I^T}{\bm{f}}-\bm{\psi^T}\pypx{\bm{R}}{\bm{f}}$$ $$\bm{G_p}=\pypx{I^T}{\bm{p}}-\bm{\psi^T}\pypx{\bm{R}}{\bm{p}}$$ 则有 \begin{equation} \label{eqs_sensitivity} \delta I=\bm{G_f}\delta\bm{f}+\bm{G_p}\delta\bm{p} \end{equation} 比如$\bm{R=Ku-f}$，有$\pypx{\bm{R}}{\bm{u}}=\bm{K}$，可得 \begin{equation}\label{adjoint} \bm{K}^T\bm{\psi}=\pypx{I}{\bm{u}} \end{equation} 这个就是得到的伴随方程。
- 伴随方程方程与有限元的基本方程$$\bm{Ku-f=0}$$ 格式上可以保持一致
- 在线性有限元问题中，$\bm{K}^T=\bm{K}$，$\bm{K}$是对称阵
- 而在非线性有限元问题里，$\bm{K}$不一定是对称阵
- 对于线性模型，由于$\bm{K}^T=\bm{K}$，因此我们称系统是自伴随的：右手边的向量$\pypx{I}{\bm{u}}$我们称为伪载荷
- 由于在求解有限元模型的位移时已经对$\bm{K}$做了LU或Cholesky分解，因此在这一步可以大大简化运算量
在设计过程中，最为重要的约束条件是结构的强度极限约束。对于每个节点列出约束方程比较费时，因此可以考虑用KS函数将所有的应力约束打包： 考虑对于每个结构有限元，有 \begin{equation} g_m=1-\frac{\sigma_m}{\sigma_y}\geq0\end{equation} 其中，$\sigma_m$是第$m$个有限元元素的von Mises应力，$\sigma_y$是材料的屈服极限。KS函数(Kresisselmeier-Steinhauser function) \begin{equation} KS=-\frac{1}{\rho}\ln[\sum_m e^{-\rho g m}] \end{equation}
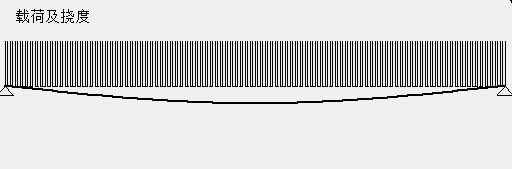
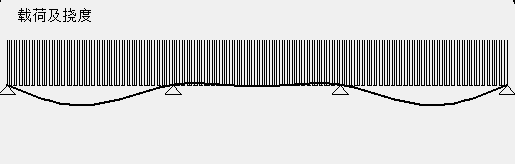
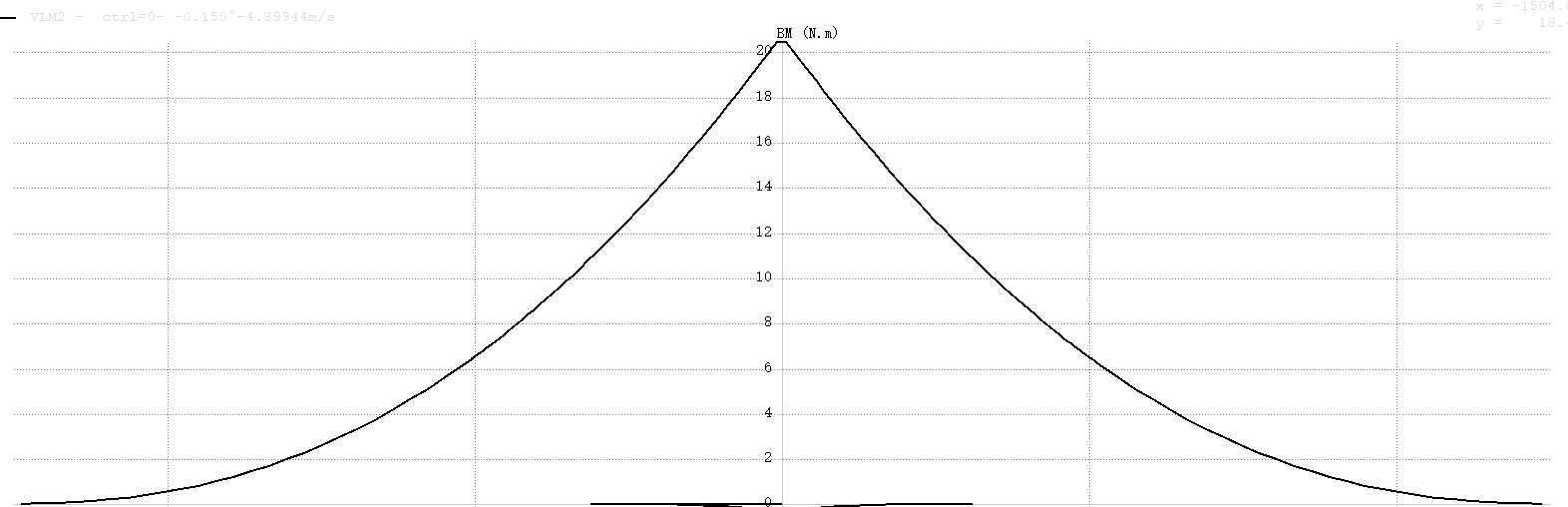
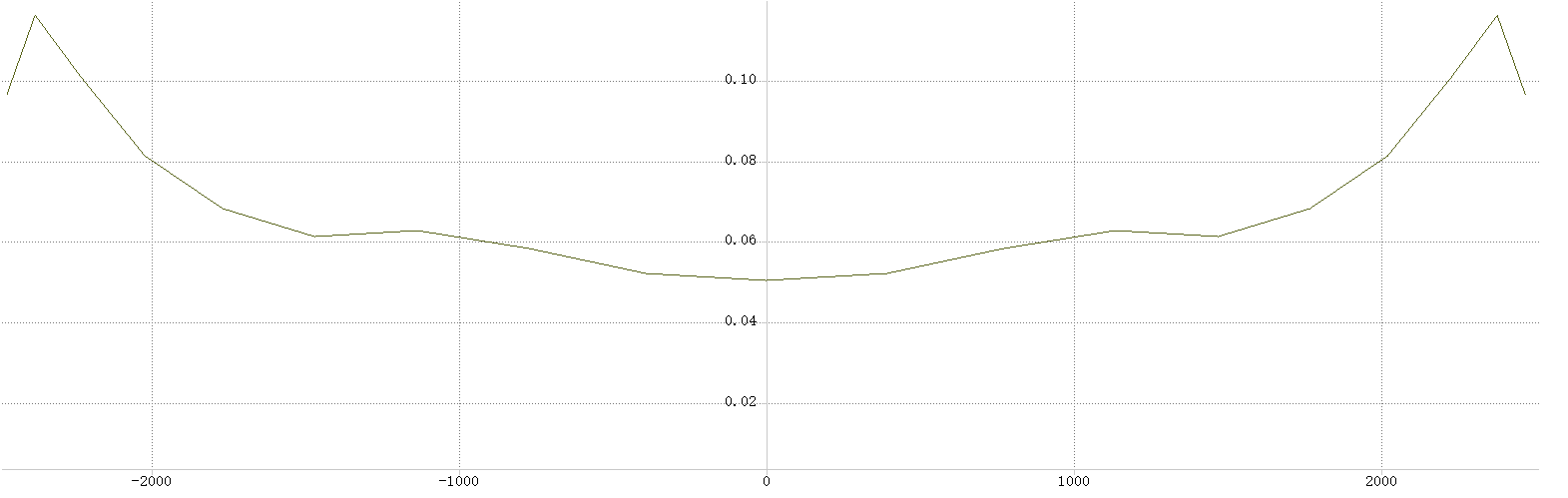
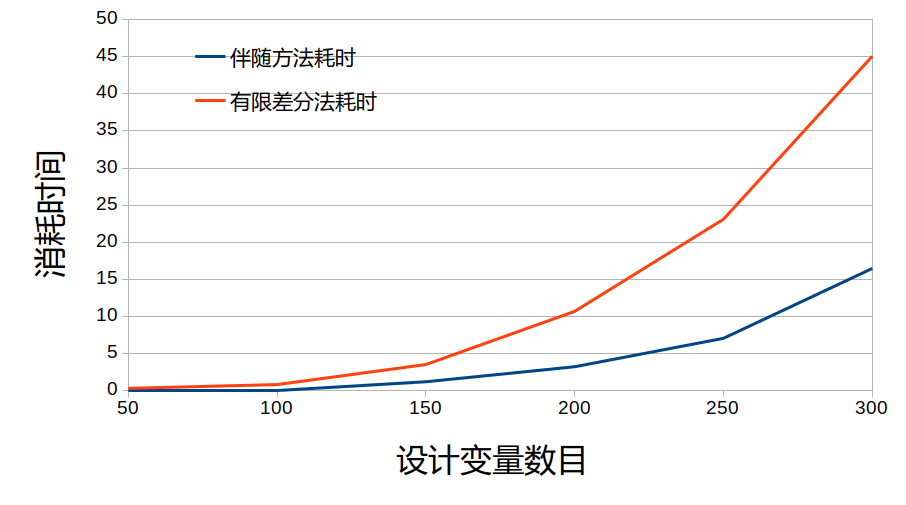
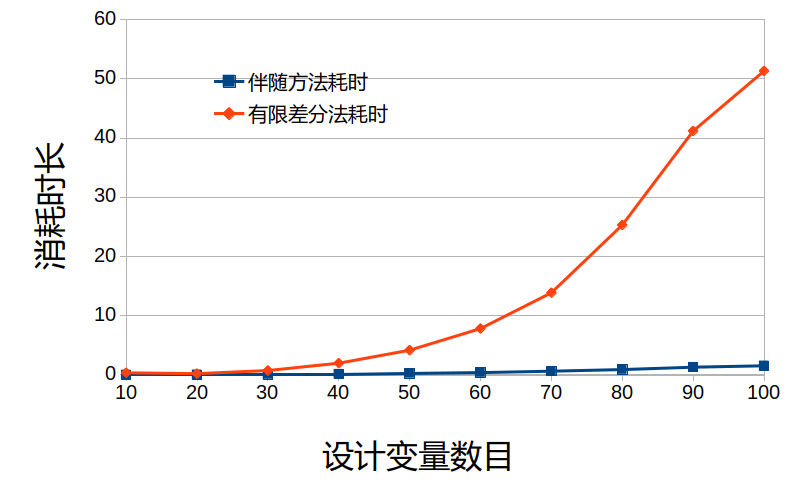
设某段矩形截面悬臂梁，长度为1米，截面宽度为1米，厚度为1米，弹性模量为6Pa，受到集度为1N/m的均部载荷。设材料的屈服应力为1.6Pa，KS函数的参数$\rho = 1$.将梁等分为若干个单元，各个单元的截面厚度为设计变量。这里应力梯度和KS函数梯度的具体推导过程略去，且KS函数梯度的表达式有两种，两种并无明显效率上的差别。通过伴随方法和有限差分法分别计算梁的应力和KS函数关于截面厚度的梯度，有限差分法计算的相对步长为%1.二种方法的计算效率对比如图所示。
有限元残差方程和气动力残差方程的伴随方程可以写成分块矩阵的形式为 \begin{equation}\label{coupled_adjoint} {\begin{bmatrix} \pypx{\bm{R}}{\bm{w}} & \pypx{\bm{R}}{\bm{u}} \\ \pypx{\bm{S}}{\bm{w}} & \pypx{\bm{S}}{\bm{u}} \end{bmatrix}}^T \begin{bmatrix} \bm{\psi} \\ \bm{\phi}\end{bmatrix} =-\begin{bmatrix}\pypx{I}{\bm{w}} \\ \pypx{I}{\bm{u}}\end{bmatrix} \end{equation}
设某段矩形机翼翼展为5米，展弦比为9，机翼梁的为圆柱形实心梁，梁的直径为0.06cm，梁的材料的弹性模量为2GPa，泊松比为0.2，材料的屈服应力为$\sigma_m=3\times10^6\text{pa}$，梁位于弦长的30%处。假设空气密度为$\rho = 1.225\text{kg}/\text{m}^2$,风速为18m/s，机翼对气流的攻角为$5^{\circ}$，机翼的升力线斜率为$5/\text{rad}$.设计变量为不同截面梁的直径。
在这里给出如下一个带约束的优化问题： \begin{align}\label{opt} \text{minimize}&\quad&I=\frac{L}{W} \notag\\ \text{w.r.t.}&\quad& \bm{p}\notag\\ \text{s.t.}&\quad& KS>0 \end{align} 和之前所给的条件一致，设某段矩形机翼翼展为5米，展弦比为9，机翼梁的为圆柱形实心梁，梁的直径为0.06cm，梁的材料的弹性模量为2GPa，泊松比为0.2，材料的屈服应力为$\sigma_m=3\times10^6\text{pa}$,梁位于弦长的30%处。假设空气密度为$\rho = 1.225\text{kg}/\text{m}^2$,风速为18m/s，机翼对气流的攻角为$5^{\circ}$，机翼的升力线斜率为$5/\text{rad}$.设计变量为不同截面梁的直径。约束条件为KS函数需要大于0，优化过程需要最小化重量与升力之比。
- 优化算法：SQP算法、移动渐近线算法
- 选取初始条件为$\bm{t}=0.06\bm{e}$
- KS函数的参数$\rho=100$
- 初始的机翼重量为$0.036$，而产生的升力为$128.306\text{N}$
- 优化后的结果为升力$L=131.472\text{N}$，升力提升了2.47%，而重量为$0.02756456959$，重量减少了23.43%
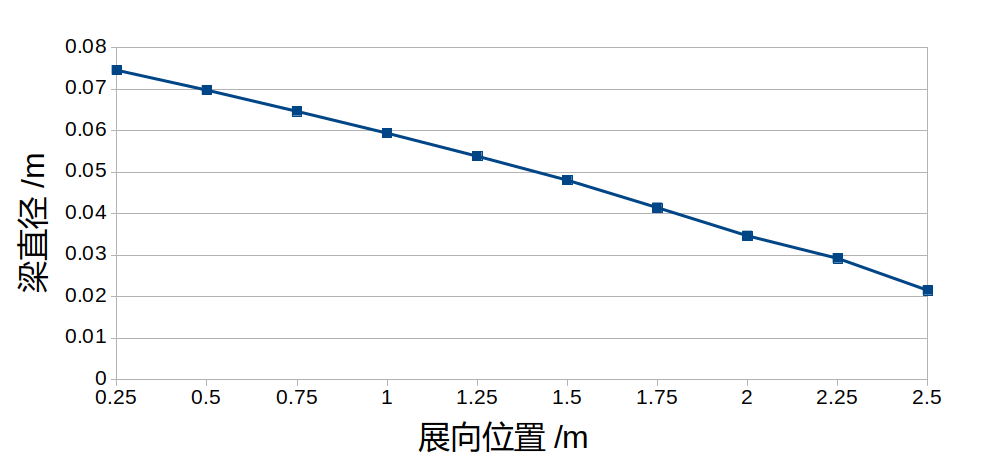
- 优化后的厚度分布为翼根较厚而翼梢较薄
- 优化前性能指标$I=0.000280579$，优化后得到的性能指标$I=0.0002096604815$，优化后的性能指标下降了25.28%
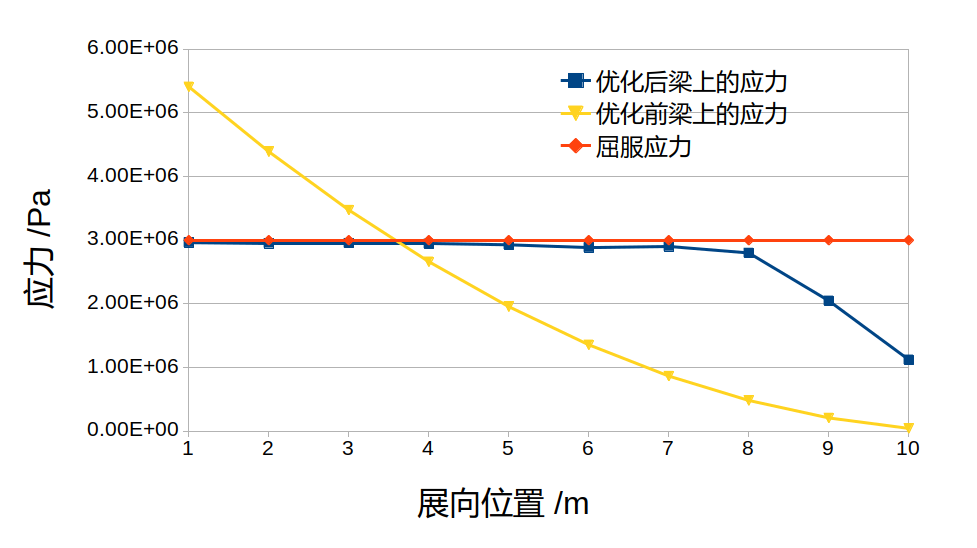
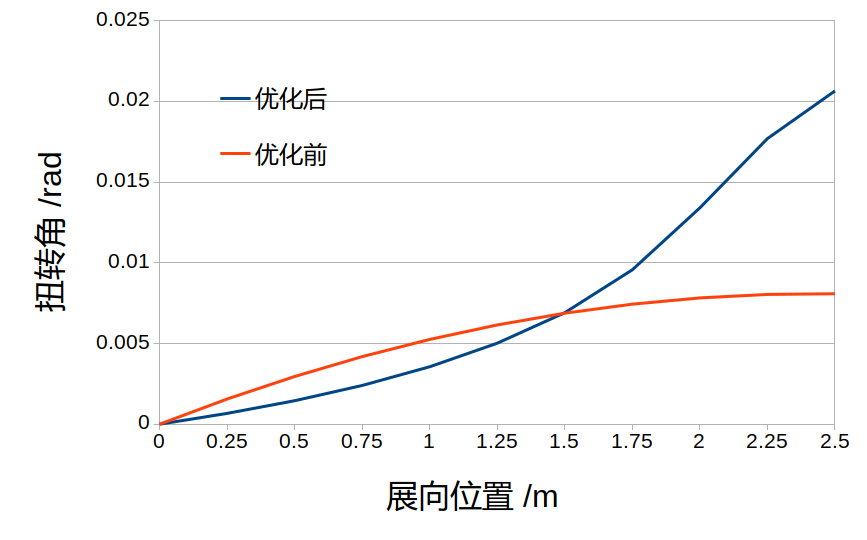
另外，由于无论是序列二次规划算法还是移动渐进线算法优化得到的结果均是局部的，因此后续工作中可以先使用一些全局搜索策略，再在局部进行基于梯度的优化。
