简要介绍PID控制器三个参数对响应的影响以及PID控制器的调节经验。
PID控制器简介
我们假设控制器应用在一个单位负反馈的闭环系统中,变量$e$代表追踪的误差,是PID控制器的输入信号。那么控制量$u$的表达式为 或
PID控制器由于其既简单又有出色性能的特点,使用在工业界95%以上的闭环控制系统中。不像其他的现代控制器需要大量的背景理论,PID控制器可以不需要大量背景知识即可调节。
PID控制器的调节参数
对一个闭环系统的响应,我们主要关注以下四个指标:
- 上升时间:$y$达到需要调节量的90%所需的时间
- 超调量
- 稳定时间
- 稳态误差
PID控制器三个参数对以上指标的影响趋势如下:
| 参数 | 上升时间 | 超调量 | 稳定时间 | 稳态误差 |
|---|---|---|---|---|
| $K_P$ | 减小 | 增大 | 无明确趋势 | 减小 |
| $K_I$ | 减小 | 增大 | 增大 | 消除 |
| $K_D$ | 无明确趋势 | 减小 | 减小 | 无明确趋势 |
典型的PID控制器调节步骤为:
- 判断控制系统中需要提升的指标
- 通过$K_P$减小上升时间
- 通过$K_D$减小超调量
- 通过$K_I$减小稳态误差
这个步骤通常在大多数场合下适用,但是我们需要找到一个合理的调节初始点,这就需要齐格勒-尼克尔斯调节法则。
齐格勒-尼克尔斯第一方法
齐格勒和尼克尔斯总结了大量的数值实验的结果,得到了多种PID控制器的调节方法。在这里介绍齐格勒-尼克尔斯第一方法,应用于系统中没有积分器以及共轭复数极点的情况,这种系统的单位阶跃响应将会是一条S型曲线。S型曲线的形状可以通过两个参数表示:延迟时间$L$和时间常数$T$,如图所示。
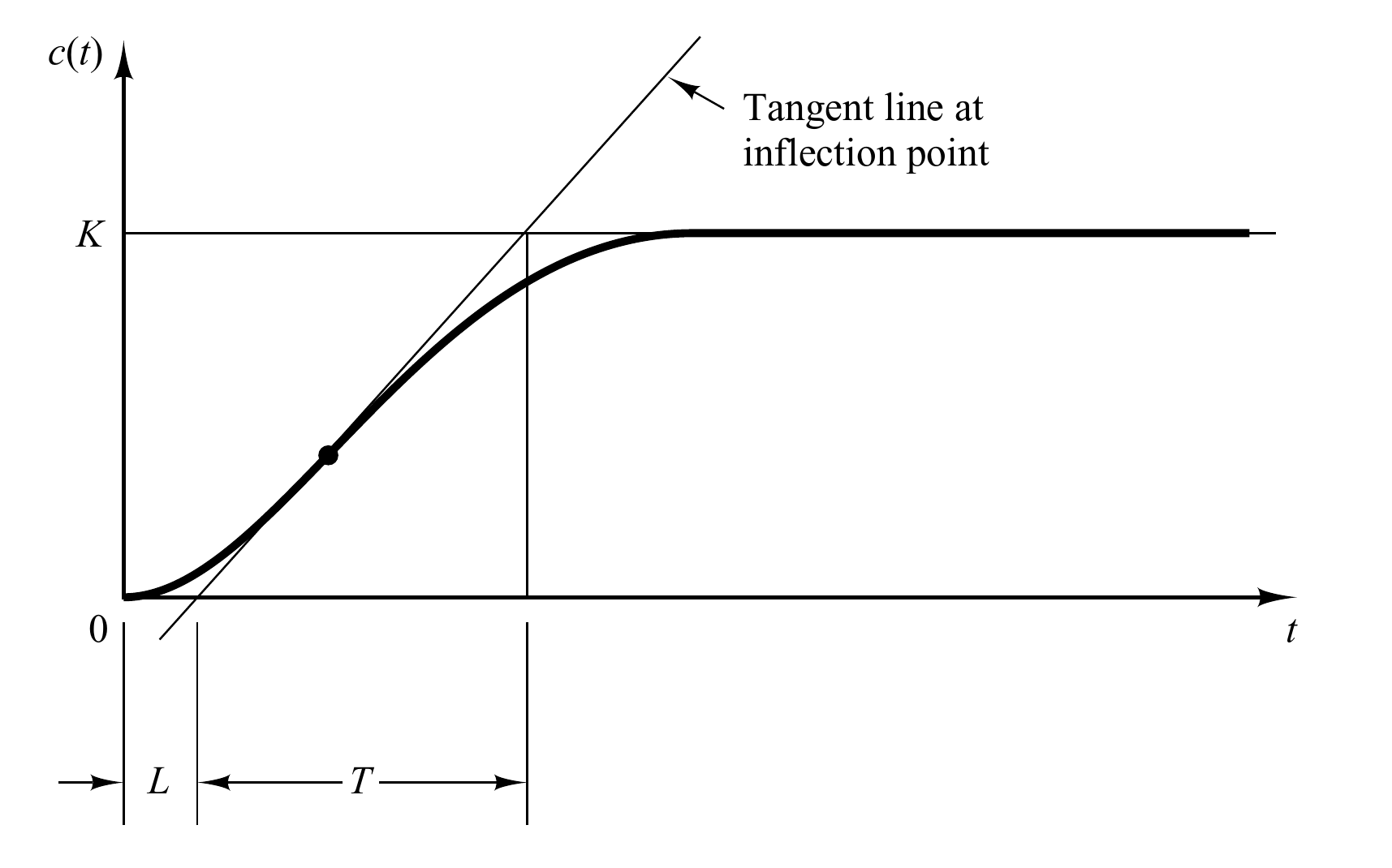
通过这两个参数,可以使用下面的公式计算PID调节的初始值:
| 控制器类型 | $K_P$ | $K_I$ | $K_D$ |
|---|---|---|---|
| P | $\frac{T}{L}$ | 0 | 0 |
| PI | $0.9\frac{T}{L}$ | $0.27\frac{T}{L^2}$ | 0 |
| PID | $1.2\frac{T}{L}$ | $0.6\frac{T}{L^2}$ | $0.6T$ |
可以验证,由齐格勒-尼克尔斯第一方法调节得到的PID控制器的极点位于原点,并在$s=-\frac{1}{L}$处有双重零点。
齐格勒-尼克尔斯第二方法
在第二方法中,我们首先令$K_I=0,K_D=0$,只使用比例控制。将$K_P$从零开始向上调节,直到达到临界值,此时系统的输出首次呈现为持续的震荡(如果无论如何调节$K_P$,系统的输出均不会呈现出可持续震荡,那么这种方法不适用)。如图所示,在$K_{cr}$的临界状态下,所对应的震荡周期为$P_{cr}$.
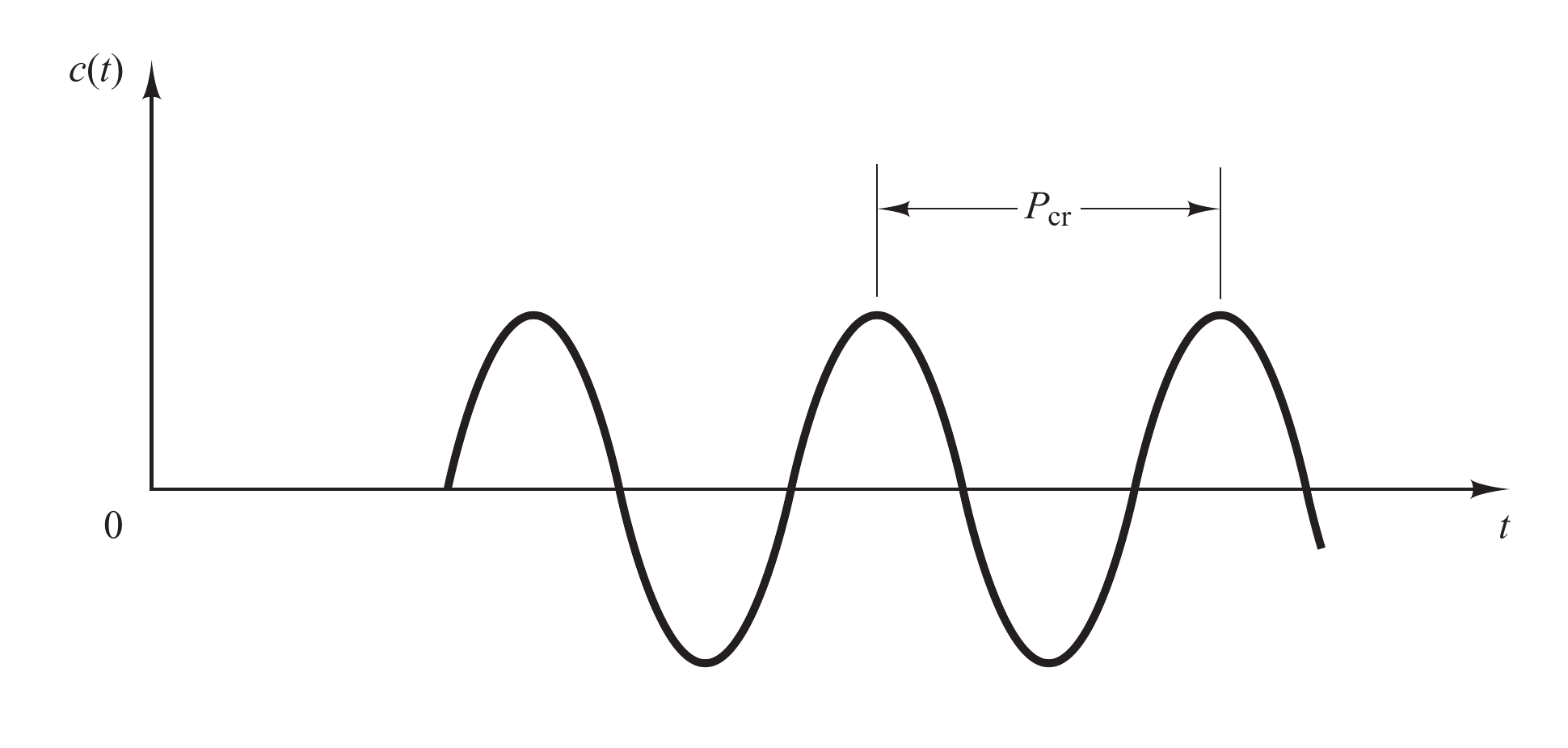
齐格勒-尼克尔斯建议的PID参数如下表所示(注意这里使用的PID参数的符号表示与上表不同):
| 控制器类型 | $K_P$ | $T_I$ | $T_D$ |
|---|---|---|---|
| P | $0.5K_{cr}$ | 0 | 0 |
| PI | $0.45K_{cr}$ | $\frac{1}{1.2}P_{cr}$ | 0 |
| PID | $0.6K{cr}$ | $0.5P_{cr}$ | $0.125P_{cr}$ |
可以验证,由齐格勒-尼克尔斯第二方法调节得到的PID控制器的极点位于原点,并在$s=-\frac{4}{P_{cr}}$处有双重零点。
如果一个系统的数学模型已知(例如传递函数),我们便可以首先使用根轨迹方法找到根轨迹上与虚轴相交的点得增益$K_{cr}$,并由虚部$\omega_{cr}$得到$P_{cr}$。
以上便是PID调节的常用经验方法。
编程实现PID调节器
这里需要注意的是,计算机实现的PID控制器必然是离散的。此外,为了避免高频噪音带来的导数项特别大,在导数项环节前面需要加一个低通滤波器。
一阶连续低通滤波器的传递函数为
在角频率为$a$时,低通滤波器输出的增益为$0.5$.写成微分方程的形式,有
转换为离散形式,由于
故得到
有点类似于上周期的输出值与此周期的观测值的加权平均值。
Pixhawk中PID控制器的C++代码如下(部分):
float PID::get_pid(float error, float scaler)
{
uint32_t tnow = AP_HAL::millis();
uint32_t dt = tnow - _last_t;
float output = 0;
float delta_time;
if (_last_t == 0 || dt > 1000) {
dt = 0;
// if this PID hasn't been used for a full second then zero
// the intergator term. This prevents I buildup from a
// previous fight mode from causing a massive return before
// the integrator gets a chance to correct itself
// 如果此PID控制器使用时间不超过1秒,将积分项先清零
reset_I();
}
_last_t = tnow;
delta_time = (float)dt / 1000.0f;
// Compute proportional component
_pid_info.P = error * _kp;
output += _pid_info.P;
// Compute derivative component if time has elapsed
if ((fabsf(_kd) > 0) && (dt > 0)) {
float derivative;
if (isnan(_last_derivative)) {
// 如果上一个周期的导数项为NaN,那么清零一些变量
// we've just done a reset, suppress the first derivative
// term as we don't want a sudden change in input to cause
// a large D output change
derivative = 0;
_last_derivative = 0;
} else {
derivative = (error - _last_error) / delta_time;
}
// 对导数项进行一阶低通滤波
// discrete low pass filter, cuts out the
// high frequency noise that can drive the controller crazy
float RC = 1/(2*M_PI*_fCut);
derivative = _last_derivative +
((delta_time / (RC + delta_time)) *
(derivative - _last_derivative));
// update state
_last_error = error;
_last_derivative = derivative;
// add in derivative component
_pid_info.D = _kd * derivative;
output += _pid_info.D;
}
// scale the P and D components
output *= scaler;
_pid_info.D *= scaler;
_pid_info.P *= scaler;
// Compute integral component if time has elapsed
// 积分项的累加
if ((fabsf(_ki) > 0) && (dt > 0)) {
_integrator += (error * _ki) * scaler * delta_time;
if (_integrator < -_imax) {
_integrator = -_imax;
} else if (_integrator > _imax) {
_integrator = _imax;
}
_pid_info.I = _integrator;
output += _integrator;
}
_pid_info.target = output;
return output;
}